Квадратичная форма — Википедия
Материал из Википедии — свободной энциклопедии
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Пусть L{\displaystyle L} есть векторное пространство над полем K{\displaystyle K} и e1,e2,…,en{\displaystyle e_{1},e_{2},\dots ,e_{n}} — базис в L{\displaystyle L}.
Функция Q:L→K{\displaystyle Q:L\to K} называется квадратичной формой, если её можно представить в виде
- Q(x)=∑i,j=1naijxixj,{\displaystyle Q(x)=\sum _{i,j=1}^{n}a_{ij}x_{i}x_{j},}
где x=x1e1+x2e2+⋯+xnen{\displaystyle x=x_{1}e_{1}+x_{2}e_{2}+\cdots +x_{n}e_{n}}, а aij{\displaystyle a_{ij}} — некоторые элементы поля K{\displaystyle K}.
- Матрицу A=(aij){\displaystyle A=(a_{ij})} называют матрицей квадратичной формы Q(x){\displaystyle Q(x)} в данном базисе. В случае, если характеристика поля K{\displaystyle K} не равна 2, можно считать, что матрица квадратичной формы симметрична, то есть aij=aji{\displaystyle a_{ij}=a_{ji}}. Так, например, квадратичную форму от двух переменных обычно записывают в виде
- Q(x1,x2)=a11x12+2a12x1x2+a22x22{\displaystyle Q(x_{1},x_{2})=a_{11}x_{1}^{2}+2a_{12}x_{1}x_{2}+a_{22}x_{2}^{2}}.
- При замене базиса (т.е. невырожденной линейной замене переменных x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}}) с матрицей замены C{\displaystyle C} матрица квадратичной формы изменяется по формуле
- A′=CTAC,{\displaystyle A’=C^{T}A\,C,}
- где A′{\displaystyle A’} — матрица квадратичной формы в новом базисе.
- Из формулы A′=CTAC{\displaystyle A’=C^{T}A\,C} следует, что определитель матрицы квадратичной формы не является её инвариантом (т.е. не сохраняется при замене базиса, в отличие, например, от матрицы линейного отображения), но её ранг — является. Таким образом, определено понятие ранга квадратичной формы.
- Если матрица квадратичной формы имеет полный ранг n{\displaystyle n}, то квадратичную форму называют невырожденной, в противном случае — вырожденной.
- Для любой квадратичной формы Q{\displaystyle Q} существует единственная симметричная билинейная форма B{\displaystyle B}, такая, что Q(x)=B(x,x){\displaystyle Q(x)=B(x,x)}. Билинейную форму B{\displaystyle B} называют полярной к Q{\displaystyle Q}, она может быть вычислена по формуле
- B(x,y)=12(Q(x+y)−Q(x)−Q(y)).{\displaystyle B(x,y)={\frac {1}{2}}\,(Q(x+y)-Q(x)-Q(y)).}
- Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.
Знакоопределённые и знакопеременные формы[править | править код]
Для решения вопроса о том, является ли данная квадратичная форма положительно (отрицательно) определённой, используется критерий Сильвестра:
- Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
- Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.
Вещественный случай[править | править код]
В случае, когда K=R{\displaystyle K=\mathbb {R} } (поле вещественных чисел), для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид (нормальный вид):
- Q(x)=x12+⋯+xp2−xp+12−⋯−xp+q2, 0≤p,q≤r,p+q=r,(∗){\displaystyle Q(x)=x_{1}^{2}+\cdots +x_{p}^{2}-x_{p+1}^{2}-\cdots -x_{p+q}^{2},\quad \ 0\leq p,q\leq r,\quad p+q=r,\qquad (*)}
где r{\displaystyle r} — ранг квадратичной формы. В случае невырожденной квадратичной формы p+q=n{\displaystyle p+q=n}, а в случае вырожденной — p+q<n{\displaystyle p+q<n}.
Для приведения квадратичной формы к каноническому виду обычно используются метод Лагранжа или ортогональные преобразования базиса, причем привести данную квадратичную форму к каноническому виду можно не одним, а многими способами.
Число q{\displaystyle q} (отрицательных членов) называется индексом инерции данной квадратичной формы, а число p−q{\displaystyle p-q} (разность между числом положительных и отрицательных членов) называется сигнатурой квадратичной формы. Отметим, что иногда сигнатурой квадратичной формы называют пару (p,q){\displaystyle (p,q)}. Числа p,q,p−q{\displaystyle p,q,p-q} являются инвариантами квадратичной формы, т.е. не зависят от способа её приведения к каноническому виду (закон инерции Сильвестра).
Комплексный случай[править | править код]
В случае, когда K=C{\displaystyle K=\mathbb {C} } (поле комплексных чисел), для любой квадратичной формы существует базис, в котором форма имеет канонический вид
- Q(x)=x12+⋯+xr2,(∗∗){\displaystyle Q(x)=x_{1}^{2}+\cdots +x_{r}^{2},\qquad (**)}
где r{\displaystyle r} — ранг квадратичной формы. Таким образом, в комплексном случае (в отличие от вещественного) квадратичная форма имеет один единственный инвариант — ранг, и все невырожденные формы имеют один и тот же канонический вид (сумма квадратов).
- Беклемишев Д. В. Аналитическая геометрия и линейная алгебра.-М.: Высш. шк. 1998, 320с.
- Гельфанд И. М., Линейная алгебра. Курс лекций.
- Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
- * Конвей Дж. Квадратичные формы, данные нам в ощущениях. — М.: МЦНМО, 2008. — 144 с. — 1000 экз. — ISBN 978-5-94057-268-8.
- Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
- Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
- Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
- Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.
Квадратичные формы
Квадратичной формойf(х1, х2,…,хn)
от n переменных называют сумму, каждый
член которой является либо квадратом
одной из переменных, либо произведением
двух разных переменных, взятым с некоторым
коэффициентом:f(х1,
х2,…,хn) =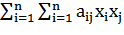
(aij=aji).
Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы. Это всегда симметрическаяматрица (т.е. матрица, симметричная относительно главной диагонали,aij=aji).
В матричной записи квадратичная форма имеет вид f(Х) = ХТAX, где
.
В самом деле
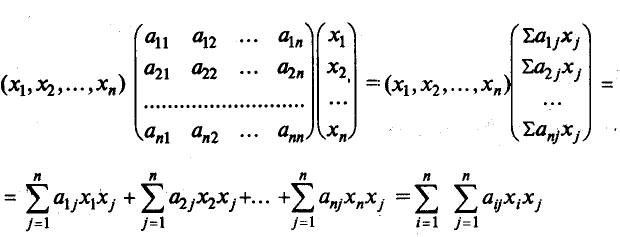
Например, запишем в
матричном виде квадратичную форму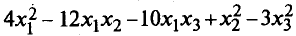 
.
Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
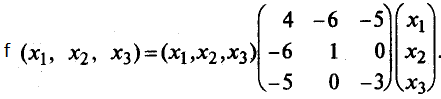
Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С — невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = ХTАХ = (CY)TA(CY) = (YTCT)A(CY) =YT(CTAC)Y.
Таким образом, при
невырожденном линейном преобразовании
С матрица квадратичной формы принимает
вид: А
Например, найдем
квадратичную форму f(y1,
y2), полученную из квадратичной
формыf(х1, х2)
= 2x12+ 4х1х2— 3х22линейным преобразованием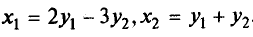 
.
Квадратичная форма
называется канонической(имеетканонический вид), если все ее
коэффициентыaij= 0 приi≠j,
т.е.f(х1,
х2,…,хn)
= a11 x12 + a22 x22+ … + ann xn2 =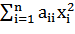 
.
Ее матрица является диагональной.
Теорема(доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования.Например, приведем к каноническому виду квадратичную форму f(х1, х2,х3) = 2x12+ 4х1х2— 3х22– х2х3.
Для этого вначале выделим полный квадрат при переменной х1:
f(х1, х2, х3) = 2(x12+ 2х1х2+ х22) — 2х22— 3х22– х2х3= 2(x1+ х2)2— 5х22– х2х3.
Теперь выделяем полный квадрат при переменной х2:
f(х1, х2, х3) = 2(x1+ х2)2– 5(х22
Тогда невырожденное линейное преобразование y1= x1+ х2,y2= х2– (1/10)х3иy3= x3приводит данную квадратичную форму к каноническому видуf(y1,y2,y3) = 2y12— 5y22— (1/20)y32.
Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами1). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называют законом инерции квадратичных форм.
Убедимся в этом,
по-другому приведя ту же квадратичную
форму к каноническому виду. Начнем
преобразование с переменной х2:f(х1,
х2,х3) = 2x12+ 4х1х2— 3х22–
х2х3= -3х22– х2х3+ 4х1х2+ 2x12= -3(х22–
— 2* х2((1/6) х3+ (2/3)х1)
+((1/6) х3+ (2/3)х1) 2) –
3((1/6) х3+ (2/3)х1) 2+ 2x12=
= -3(х2– (1/6) х3— (2/3)х1)2–
3((1/6) х3+ (2/3)х1)
Также следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичную форму f(X) называютположительно(отрицательно)определенной, если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е.f(X) > 0 (отрицательна, т.е.f(X) < 0).
Например, квадратичная форма f1(X) = x12+ х22— положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная формаf2(X) = -x12+ 2x1х2— х22— отрицательно определенная, т.к. представляет ее можно представить в видеf2(X) = -(x1— х2)2.
В большинстве практических ситуации установить знакоопределенность квадратичной формы несколько сложнее, поэтому для этого используют одну из следующих теорем (сформулируем их без доказательств).
Теорема. Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все собственные значения ее матрицы положительны (отрицательны).
Теорема (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры матрицы этой формы положительны.
Главным (угловым)
миноромk-го порядка
матрицы Аn-го порядка
называют определитель матрицы,
составленный из первыхkстрок и столбцов матрицы А (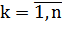
).
Отметим, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, причем минор первого порядка должен быть отрицательным.
Например, исследуем на знакоопределенность квадратичную форму f(х1, х2) = 2x12+ 4х1х2+ 3х22.
Способ 1. Построим
матрицу квадратичной формы А =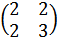 
.
Характеристическое уравнение будет
иметь вид
=
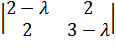(2 -)*
*(3 -)
– 4 = (6 — 2- 3+ 2) – 4 =2— 5+ 2 = 0;D= 25 – 8 = 17;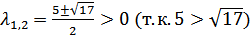
. Следовательно, квадратичная форма –
положительно определенная.
Способ 2. Главный минор
первого порядка матрицы А 1=a11= 2 > 0. Главный
минор второго порядка2=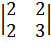
= 6 – 4 = 2 > 0. Следовательно, по критерию
Сильвестра квадратичная форма –
положительно определенная.
Исследуем на знакоопределенность другую квадратичную форму, f(х1, х2) = -2x12+ 4х1х2— 3х22.
Способ 1. Построим
матрицу квадратичной формы А =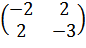 
.
Характеристическое уравнение будет
иметь вид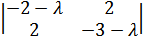
. Следовательно, квадратичная форма –
отрицательно определенная.
Способ 2. Главный минор
первого порядка матрицы А 1=a11=
= -2 < 0. Главный
минор второго порядка2=
= 6 – 4 = 2 > 0. Следовательно, по критерию
Сильвестра квадратичная форма –
отрицательно определенная (знаки главных
миноров чередуются, начиная с минуса).
И в качестве еще одного примера исследуем на знакоопределенность квадратичную форму f(х1, х2) = 2x12+ 4х1х2— 3х22.
Способ 1. Построим
матрицу квадратичной формы А =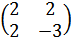 
.
Характеристическое уравнение будет
иметь вид
=
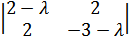(2 -)*
*(-3 -)
– 4 = (-6 — 2+ 3+2) – 4 =2+- 10 = 0;D= 1 + 40 = 41;
. Одно из этих чисел отрицательно, а
другое – положительно. Знаки собственных
значений разные. Следовательно,
квадратичная форма не может быть ни
отрицательно, ни положительно определенной,
т.е. эта квадратичная форма не является
знакоопределенной (может принимать
значения любого знака).
Способ 2. Главный минор
первого порядка матрицы А 1=a11= 2 > 0. Главный
минор второго порядка2=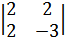
= -6 – 4 = -10 < 0. Следовательно, по критерию
Сильвестра квадратичная форма не
является знакоопределенной (знаки
главных миноров разные, при этом первый
из них – положителен).
1Рассмотренный способ приведения квадратичной формы к каноническому виду удобно использовать, когда при квадратах переменных встречаются ненулевые коэффициенты. Если их нет, осуществить преобразование все равно возможно, но приходится использовать некоторые другие приемы. Например, пустьf(х1, х2) = 2x1х2= x12+ 2x1х2 + х22— x12— х22=
= (x1+ х2)2— x12— х22= (x1+ х2)2– (x12— 2x1х2 + х22) — 2x1х2 = (x1+ х2)2– — (x1— х2)2— 2x1х2; 4x1х2= (x1+ х2)2– (x1— х2)2;f(х1, х2) = 2x1х2= (1/2)* *(x1+ х2)2– (1/2)*(x1— х2)2=f(y1,y2) = (1/2)y12– (1/2)y22, гдеy1= х1+ х2, аy2= х1– х2.
Квадратичные формы
КВАДРАТИЧНЫЕ ФОРМЫ И ИХ ПРИМЕНЕНИЯ
Определение. Квадратичной формой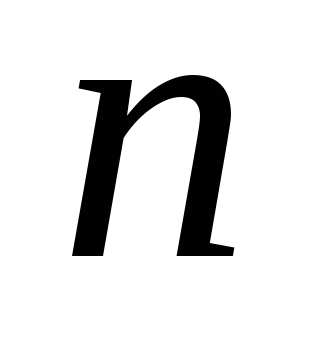 
переменных 
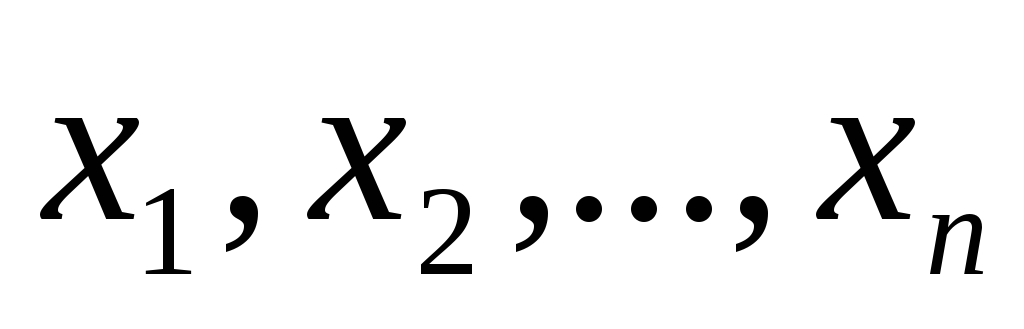,принимающих
числовые значения ,
называется числовая
функция вида
,
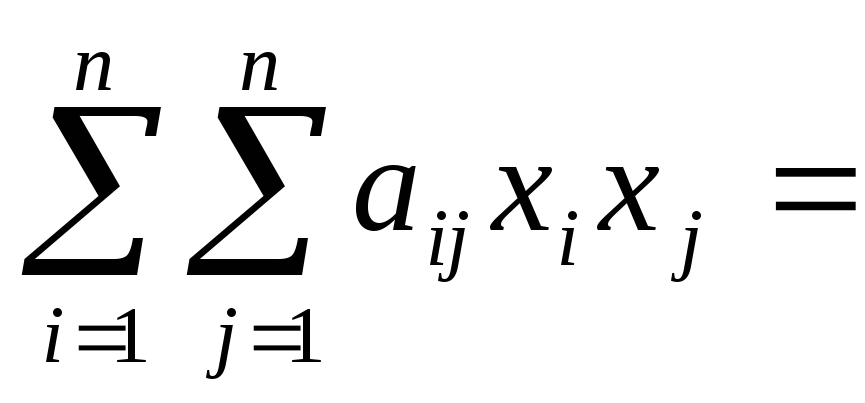
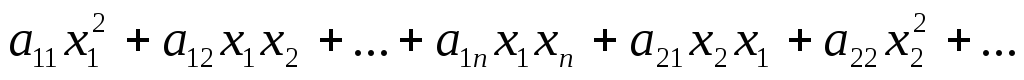
где 
—
числа,
называемые коэффициентами квадратичной
формы.
Определение. Матрицей квадратичной формы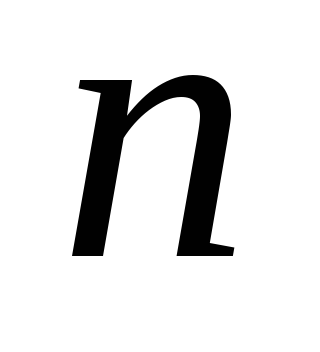 
переменных 
,
называется симметрическая матрица
порядка 
,
элементы главной диагонали которой
совпадают с коэффициентами при квадратах
переменных,
а каждый недиагональный элемент,
расположенный в 
ой
строке 
ом
столбце,
равен половине коэфициента при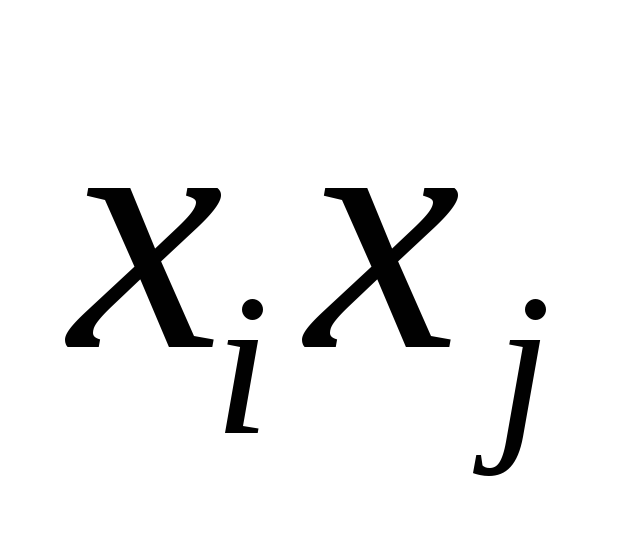 
в квадратичной форме.
Определение. Рангом квадратичной формы называется
ранг её матри-цы.
Квадратичная форма может быть записана
в матричном ви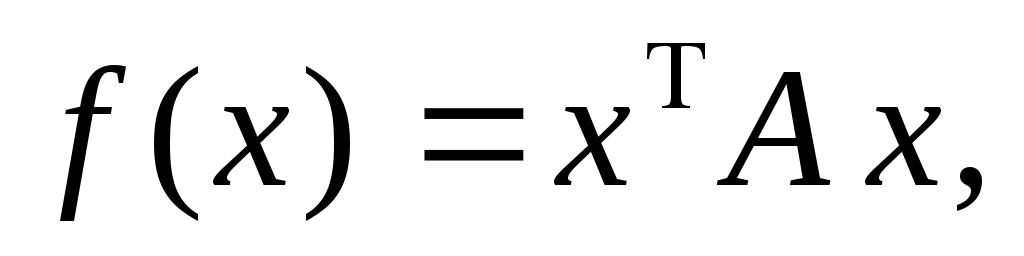де 
где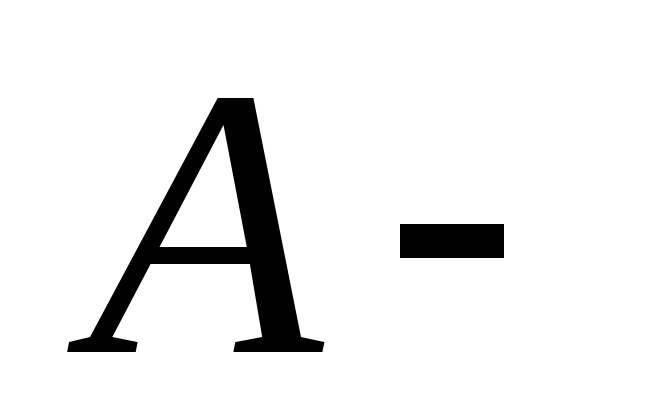 
матрица
квадратичной формы и 
.
Определение.
Квадратичная форма называется канонической
(имеет канонический вид),
если коэфициенты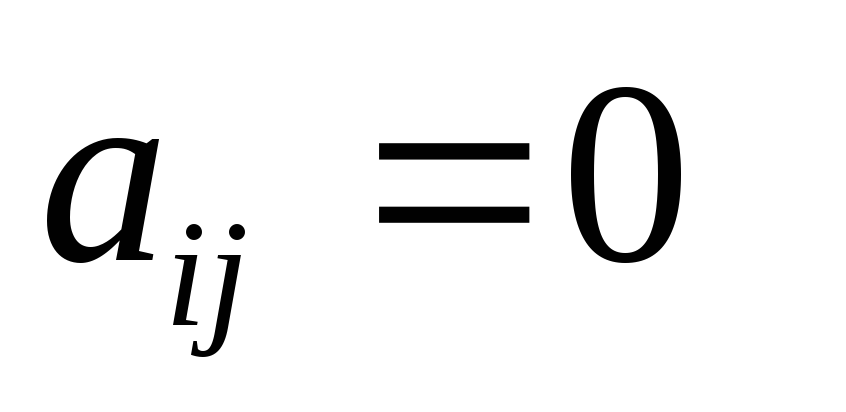 
при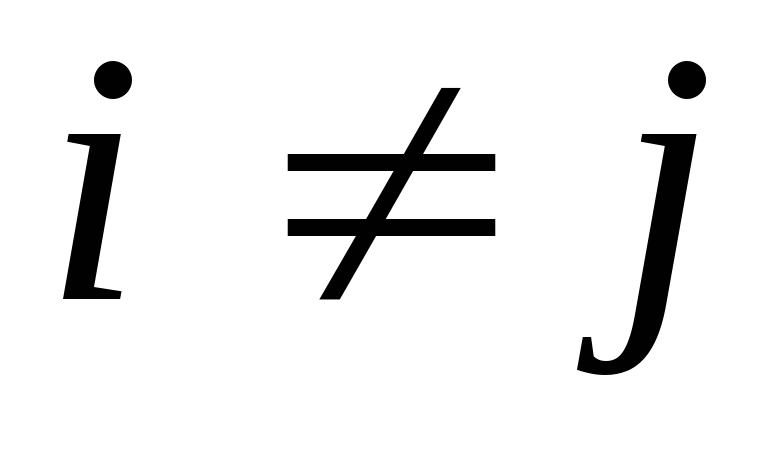 
,
то есть,
если матрица квадратичной формы
диагональная и следовательно
.,
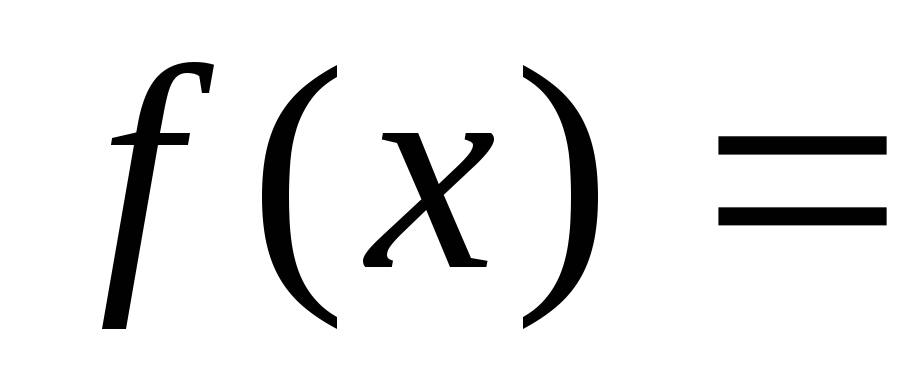
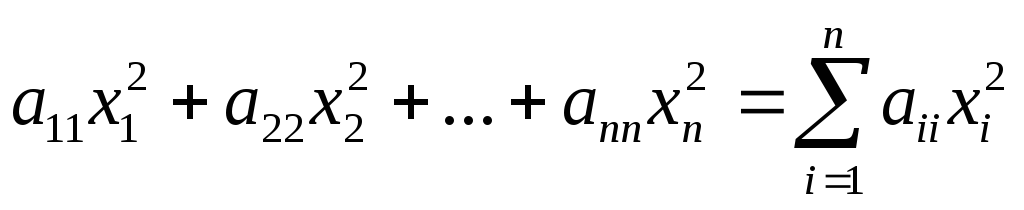где
не все коэффициенты 
равны
нулю.
Теорема (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.
Определение.
Нормальным
видом квадратичной
формы называется такой канонический
вид,
в котором коэффициенты при квадратах
неизвестных (не считая нулевых) равны 
.
Определение.
Квадратичная
форма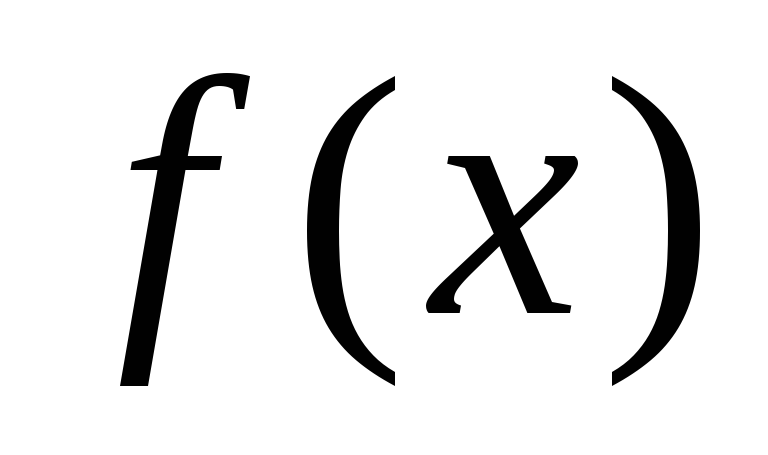 
называется положительно
(отрицательно)
определённой, если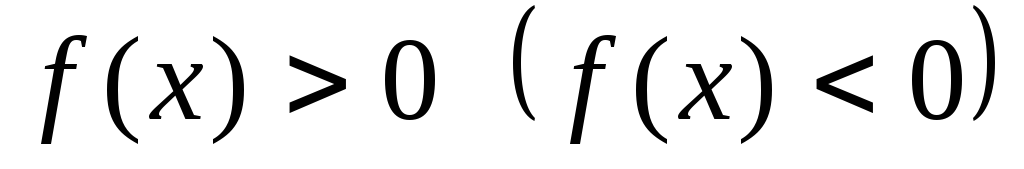 
при всех
108
и
положительно (отрицательно)
полуопределённой,если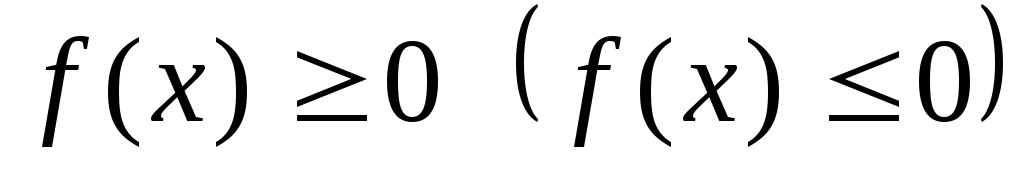 
при всех 
.
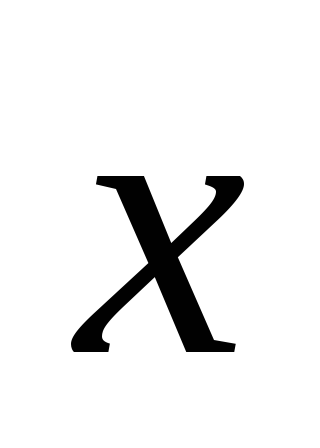Теорема (критерий
Сильвестра).
Для того чтобы квадратичная
форма 
была положительно определённой,
необходимо и достаточно
чтобы все угловые миноры матрицы
квадратичной
формы
были положительны,то
есть,
чтобы
Здесь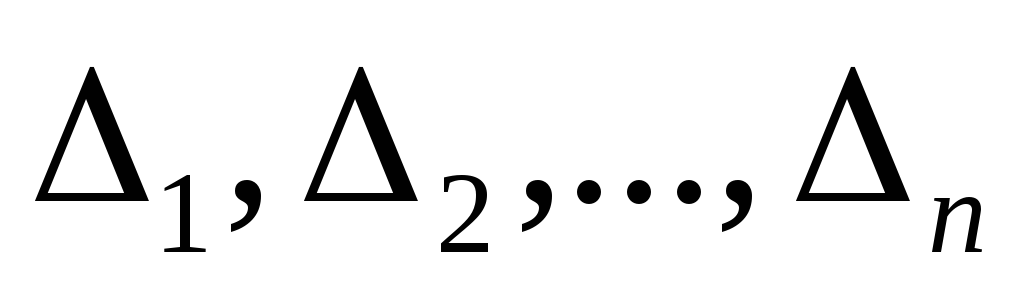 
-угловые
миноры матрицы квадратичной
формы.
Следствие.
Для того чтобы квадратичная
форма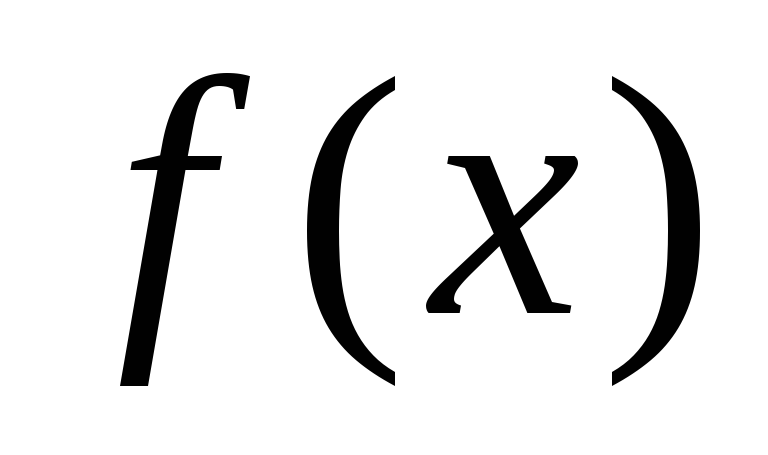 
была отрицательно определённой,
необходимо и достаточно,
чтобы знаки угловых миноров матрицы
квадратичной
формы чередовались следующим образом: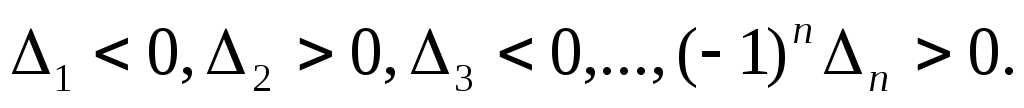 
Примеры
1. Привести квадратичную форму к каноническому виду методом Лагранжа и записать соответствующее преобразование
.
Решение. Следуя алгоритму метода Лагранжа,
выделим вначале в квад-ратичной форме
все члены, содержащие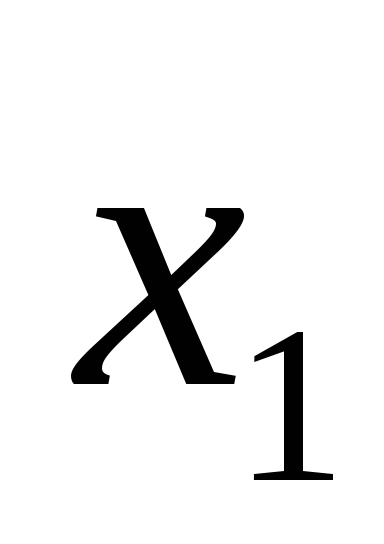 
,
и дополним их до полного квадрата:
.
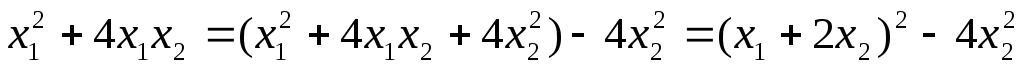Сделаем
в этом выражении замену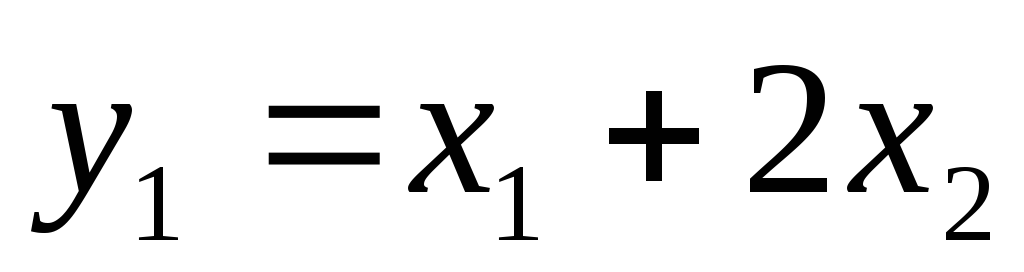 
и подставим его в квадратичную форму.
Получим:
.
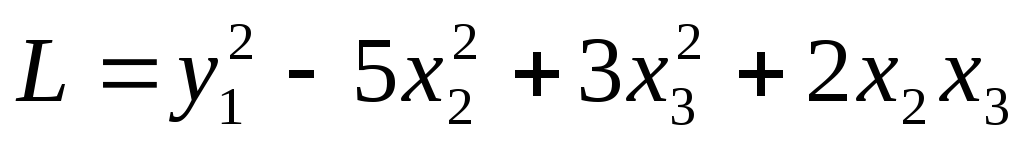Далее
выделим в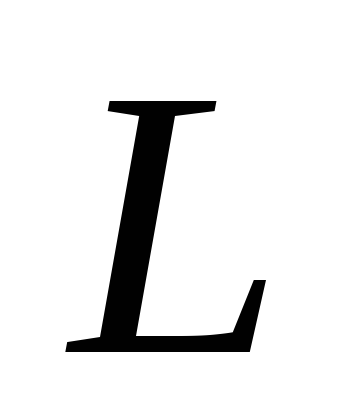 
члены, содержащие 
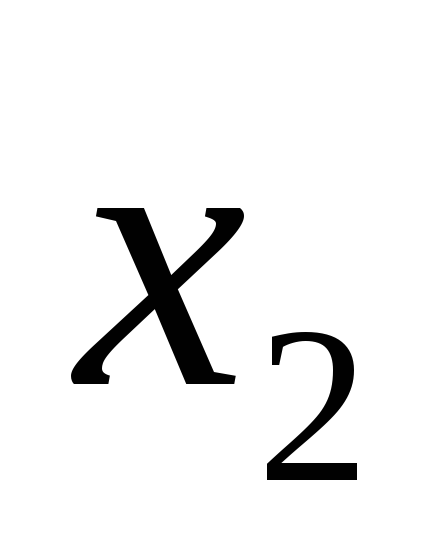и проделаем с ними анало-гичную процедуру:
Если
положить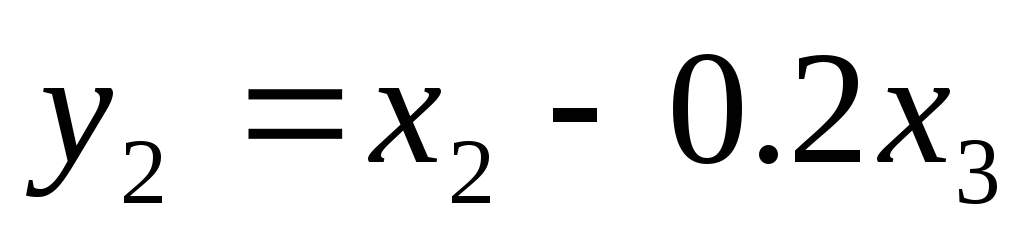 
,
то квадратичная форма уже не будет
содержать смешанных произведений.
Примем также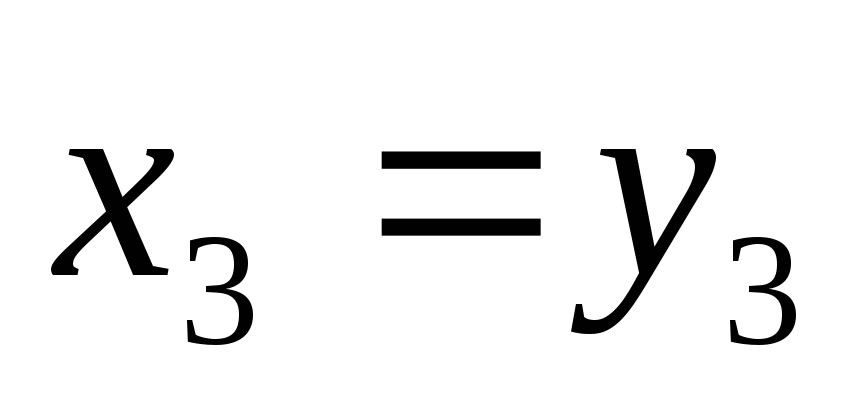 
,
тогда
109
канонический вид квадратичной формы есть
.
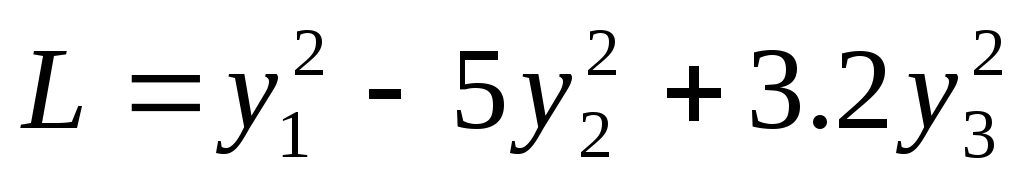Соответствующее
преобразование от переменных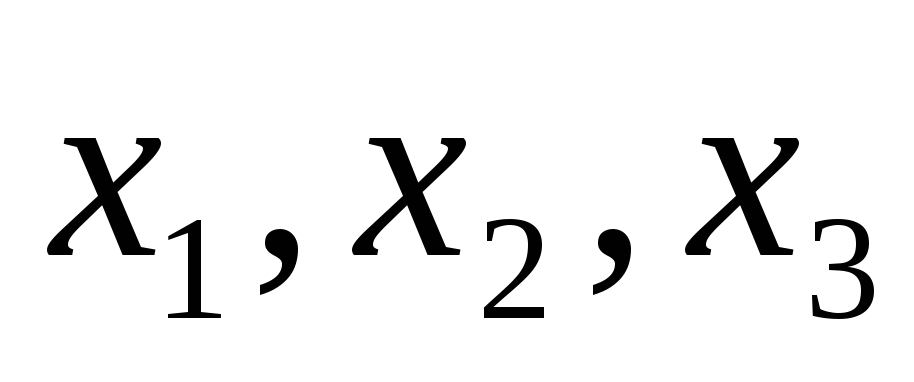 
к переменным 
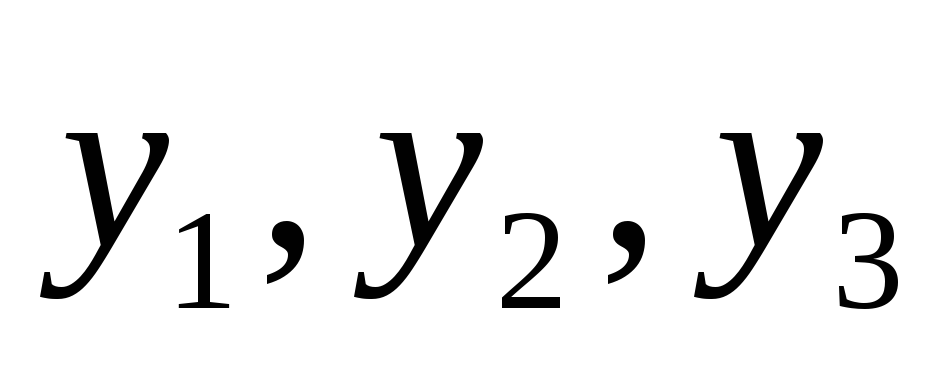имеет вид:
.
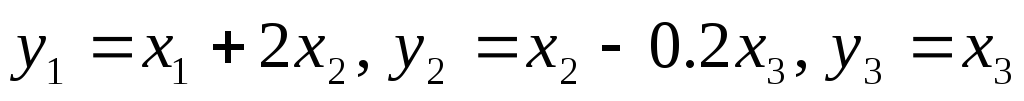2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий канонический вид этой формы:
.
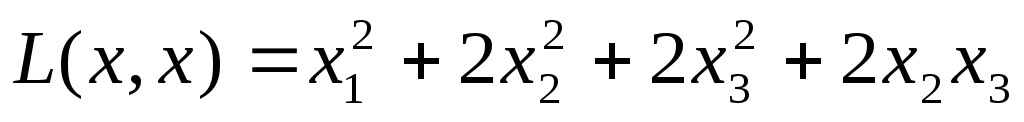Решение. В исходном базисе 
матрица оператора, соответствующая
данной квадратичной форме, есть
.
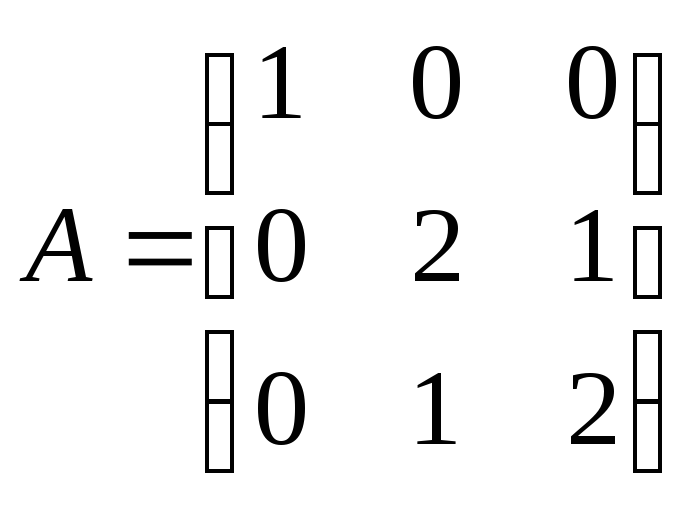Эта
матрица будет определять
квадратичную форму канонического вида
в ортонормированном базисе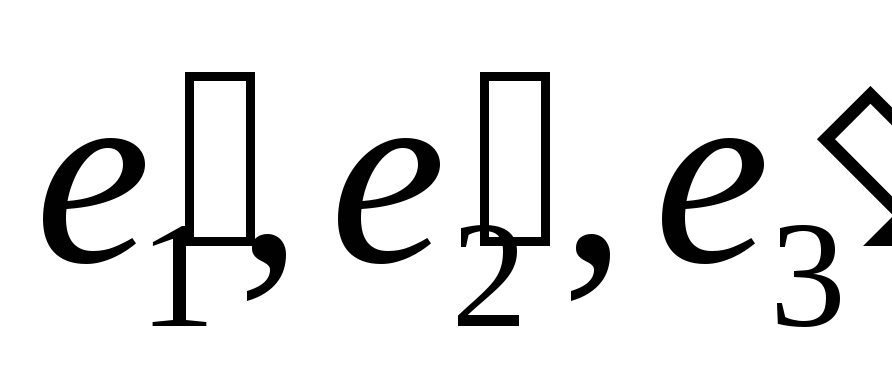 
,
составленном из собственных векторов
матрицы 
.
Найдем их.
Характеристическое
уравнение для матрицы 
имеет вид
.
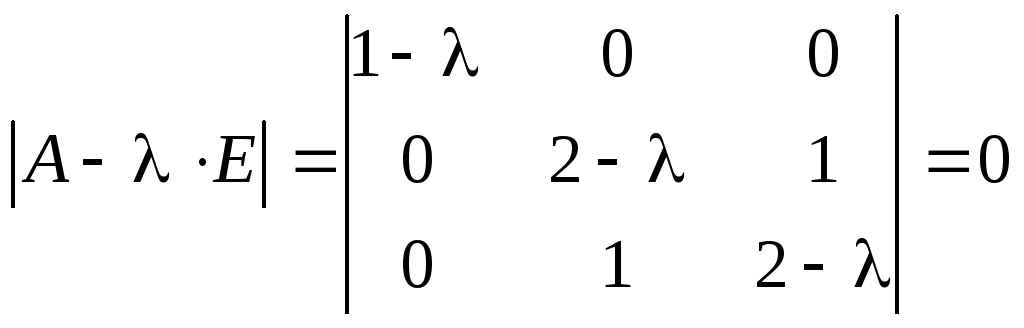Откуда следует
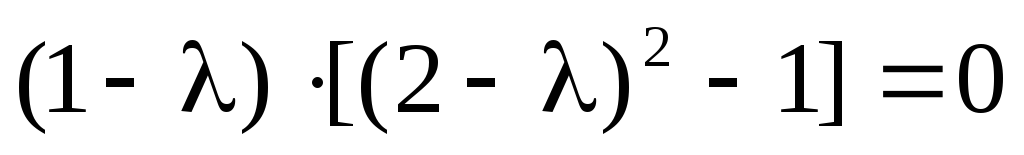и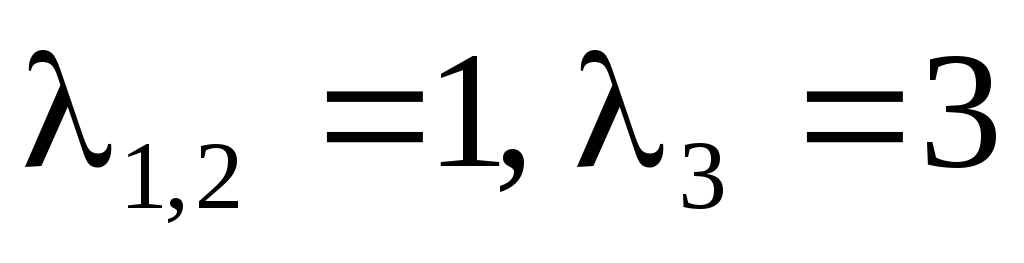 
.
Как известно собственные векторы матрицы находятся из уравнений
.
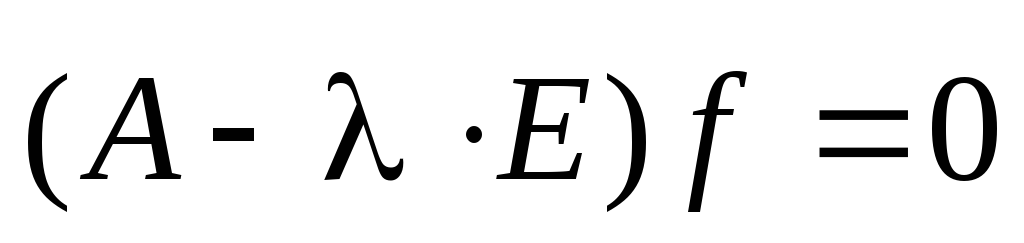Для
случая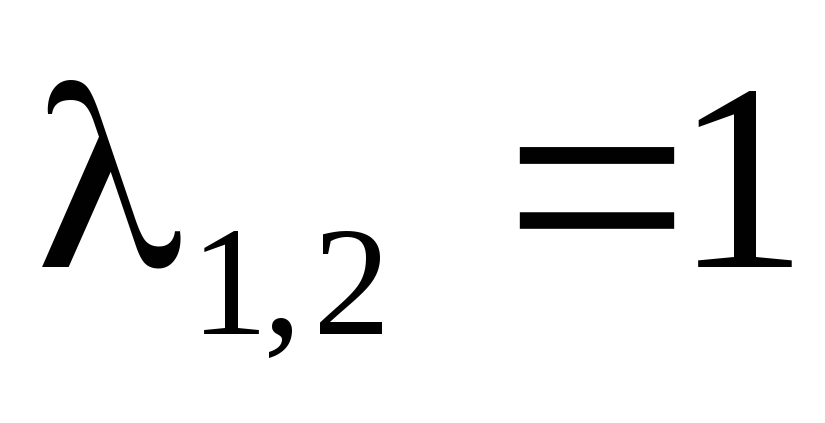 
имеем:
.
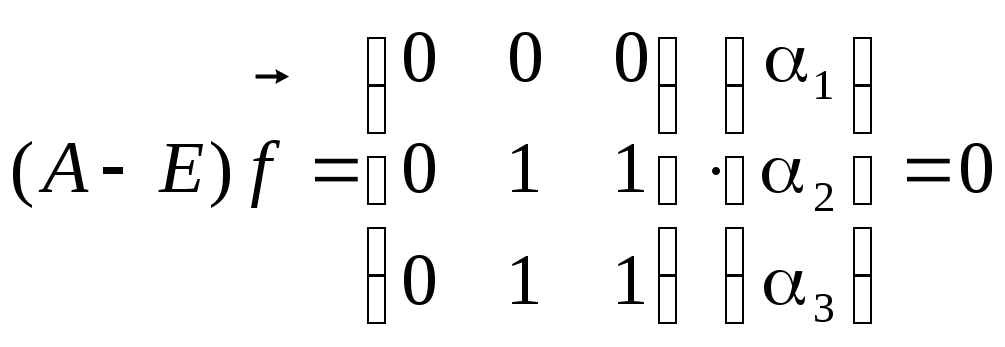110
Ранг
матрицы этой системы уравнений
(относительно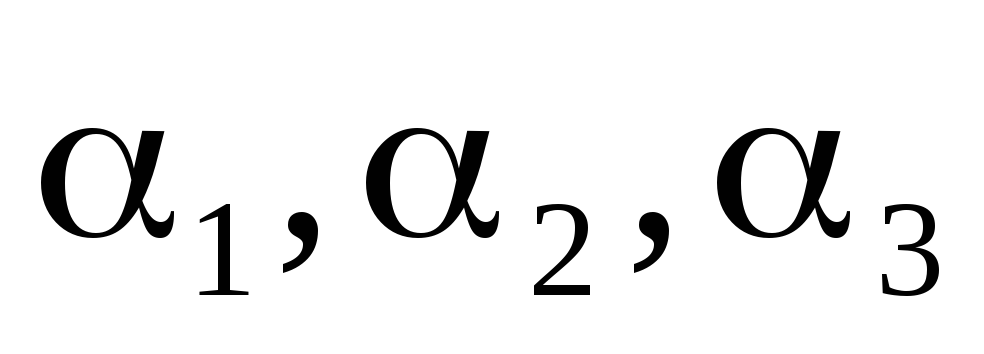 
)
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
Как
видно из данной системы, величина 
принимает произвольные значения, а
величины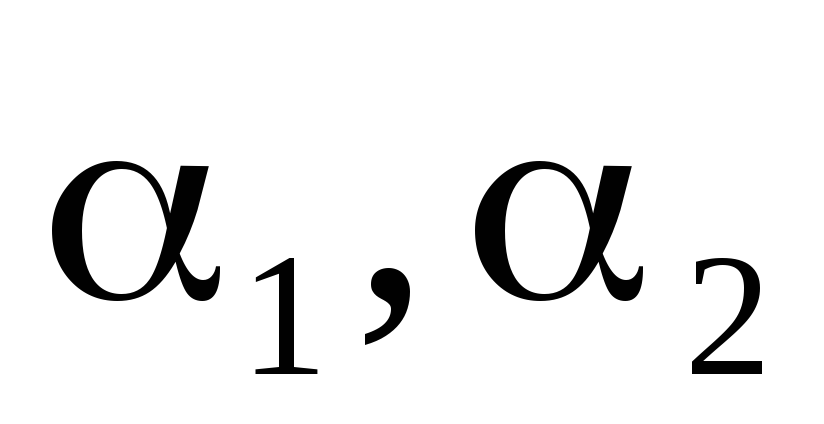 
связаны соотношением 
.
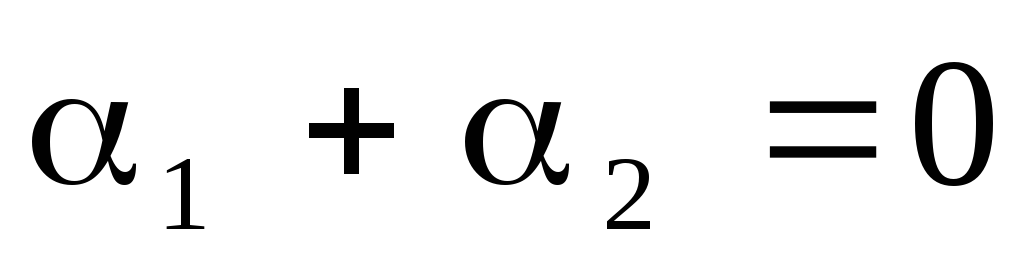В качестве собственных можно выбрать,
например, векторы
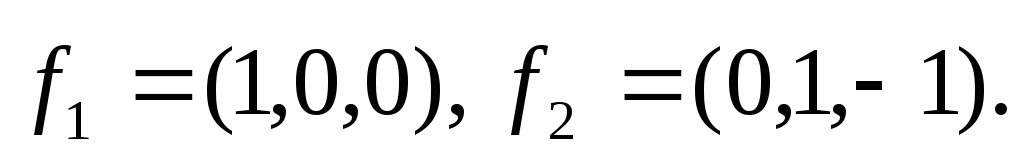
Эти
векторы ортогональны: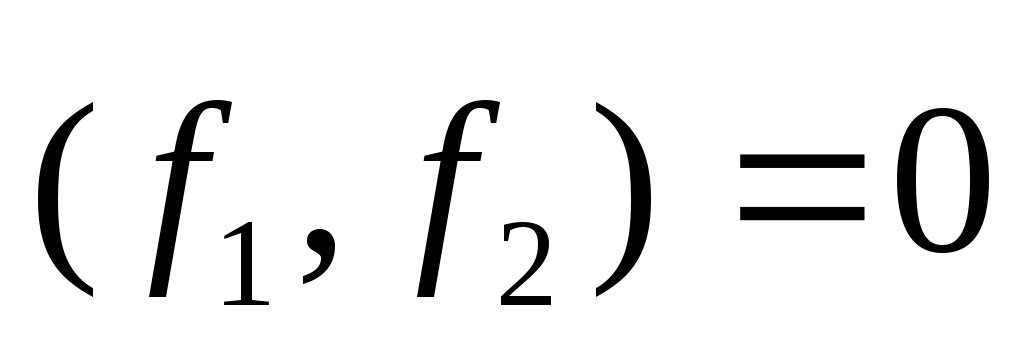 
(если бы они оказались не ортогональными,
то их нужно было бы ортогонализировать
с помощью стандартной процедуры). Вектор 
к тому же и нормирован. Откуда следует
— 
.
Нормируем теперь вектор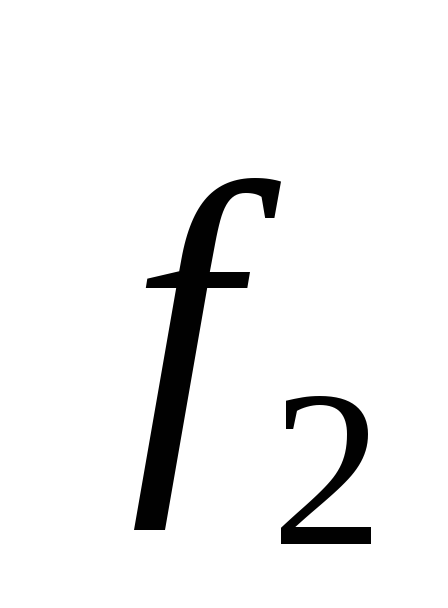
:
.
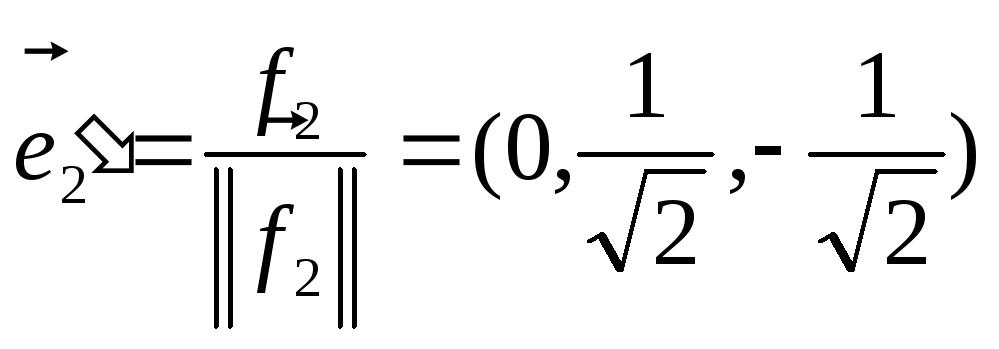Для
случая 
уравнение, определяющее собственный
вектор есть
.
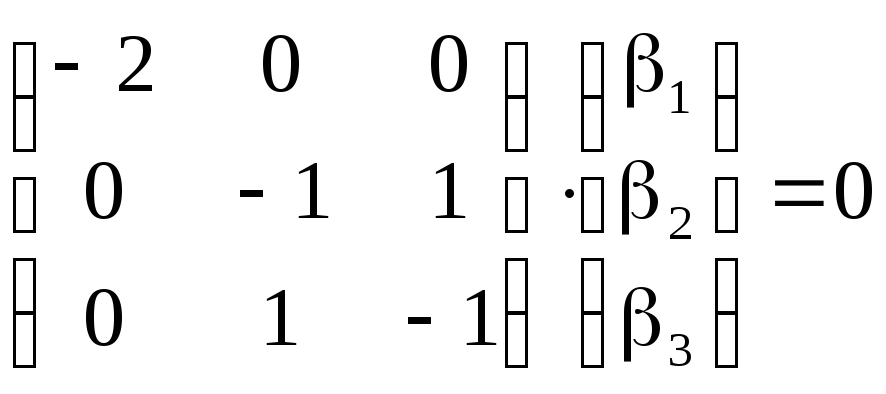Ранг
матрицы этой системы уравнений равен
2. Следовательно она имеет одно линейно
независимое решение, например, 
Отнормируем этот вектор: 
.
Теперь можно составить искомую матрицу ортогонального преобразования:
.
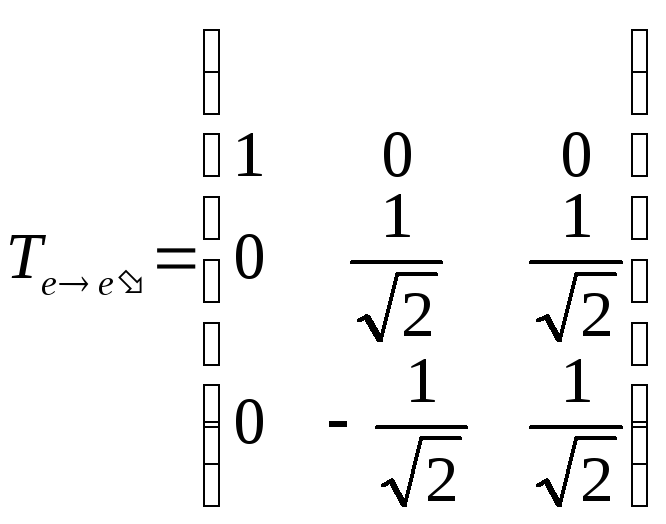111
Исходная квадратичная форма будет иметь следующий канонический вид
.
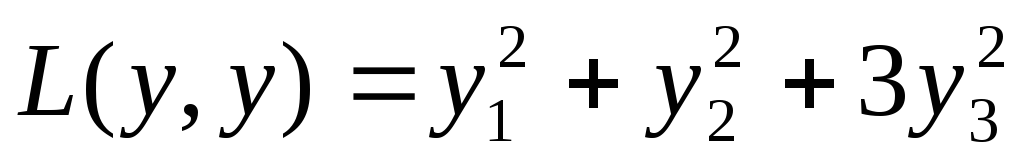При
этом переменные 
связаны с переменными 
соотношением
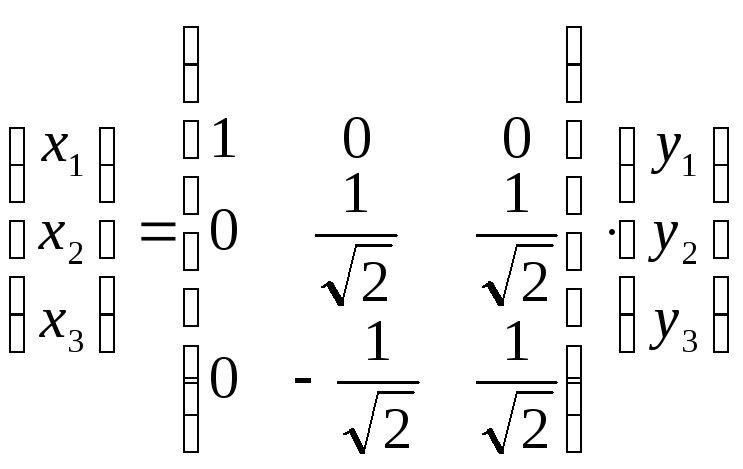или
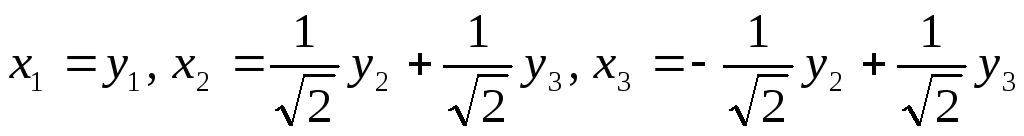
3. Построить в прямоугольной системе координат фигуру, определяемую следующим уравнением, предварительно приведя его к каноническому виду
.
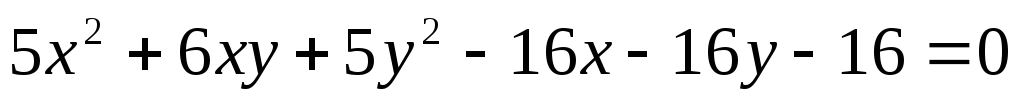Решение. Выделим в этом выражении квадратичную
форму 
.
Это три первых слагаемых уравнения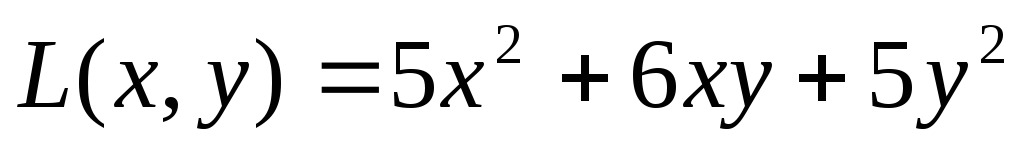 
.
Матрица
квадратичной формы равна 
.
Проведём процедуру приведения квадратичной
формы к каноническому виду с помощью
ортогонального преобразования.
Характеристическое уравнение матрицы
имеет вид
.
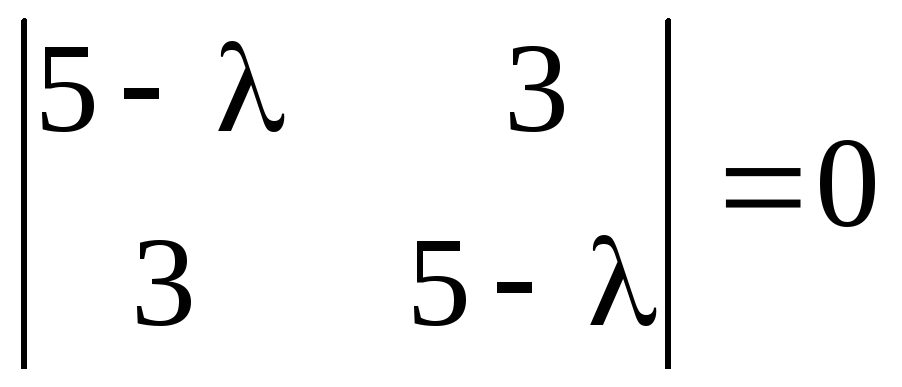Его
корни таковы: 
.
Найдём
теперь собственные векторы, соответствующие
этим корням и отнормрируем их. Для
вектора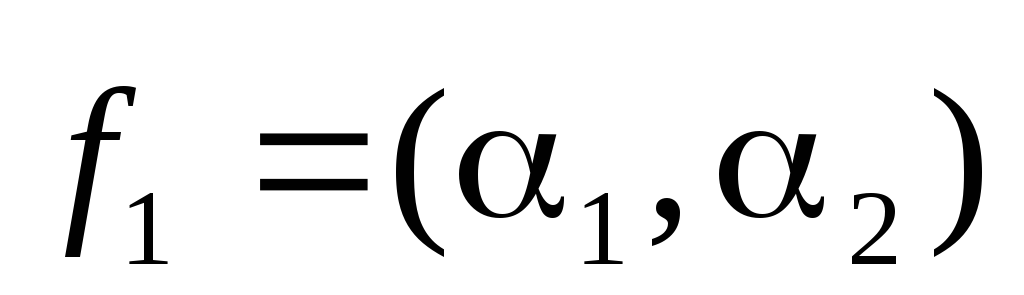 
,
соответствующего
,
имеем
112
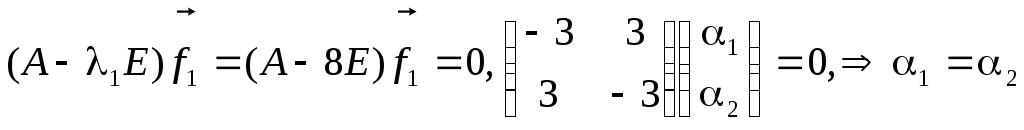
В
итоге собственный вектор, соответствующий 
,
можно выбрать в виде
.
Анологичная
процедура для собственного вектора
даёт: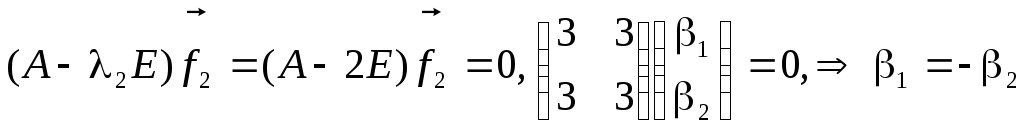 
Откуда:
.
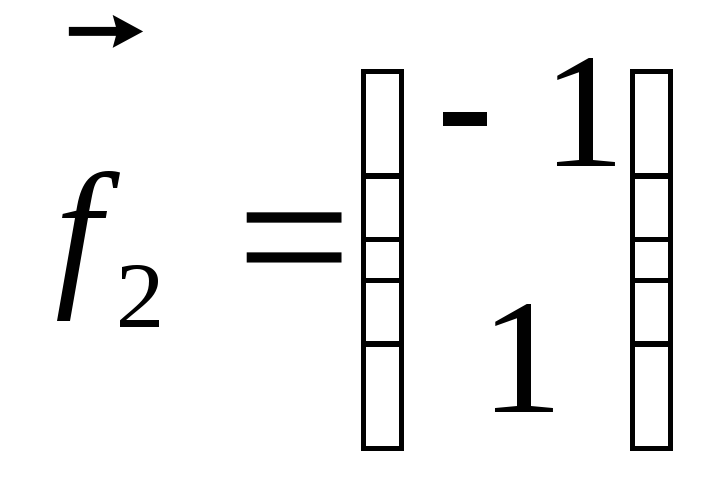После нормировки полученных векторов имеем:
.
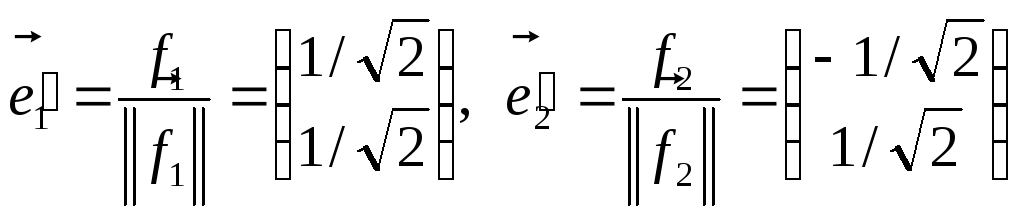Эти
векторы представляют собой ортонормированный
базис новой системы координат. Матрица
ортогонального оператора, приводящего
квадратичную форму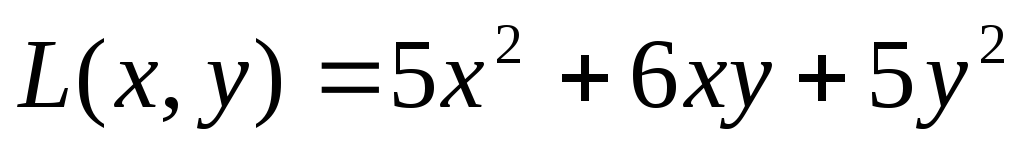 
к каноническому виду 
,
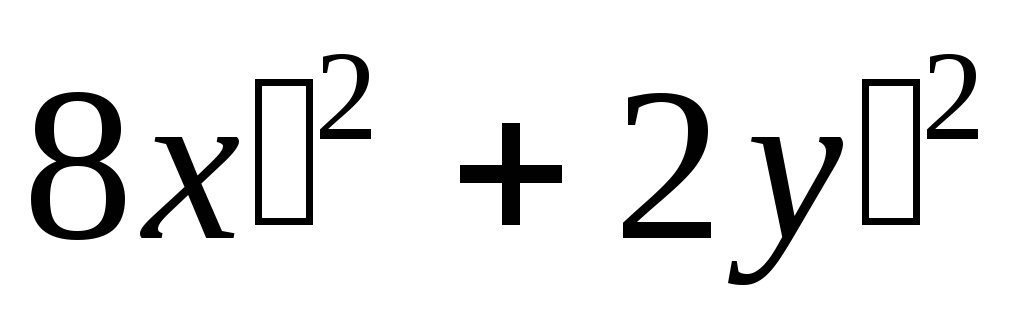есть
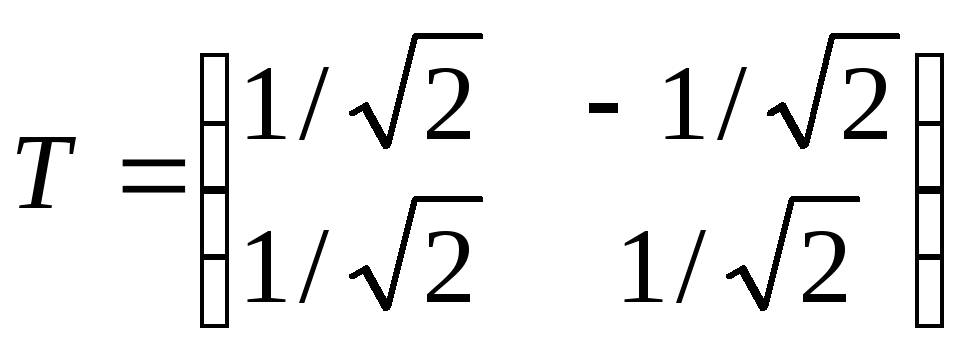
Связь
старых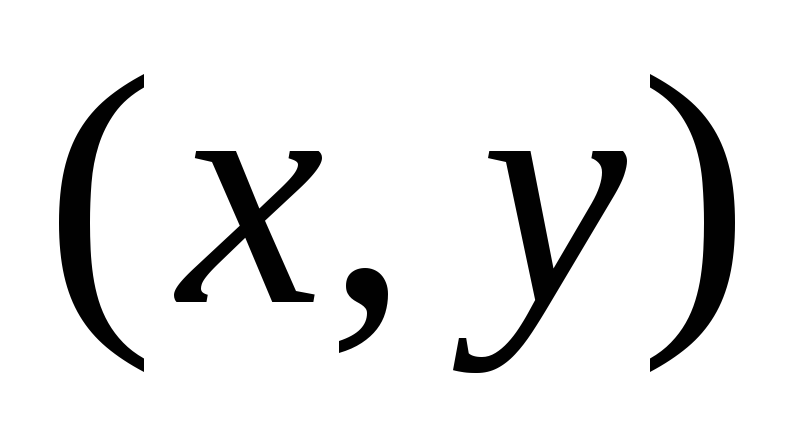 
и новых 
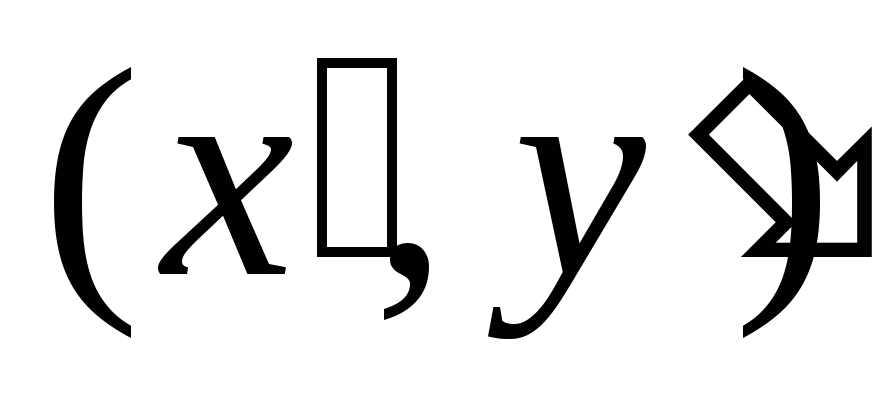координат определяется соотношением 
.
Учитывая приведенные выражения, приведём заданную квадратичную форму к каноническому виду
113
Это
есть каноническое уравнение эллипса в
системе координат 
,которая
получается из исходной её поворотом на
угол 
и
переносом начала координат в точку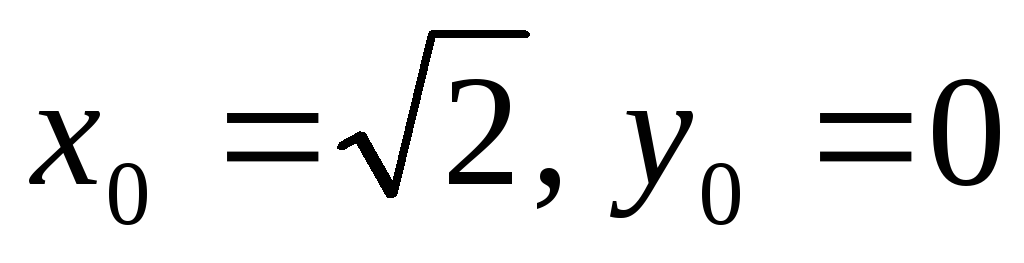 
.
Записать матрицу квадратичной формы:
5.1.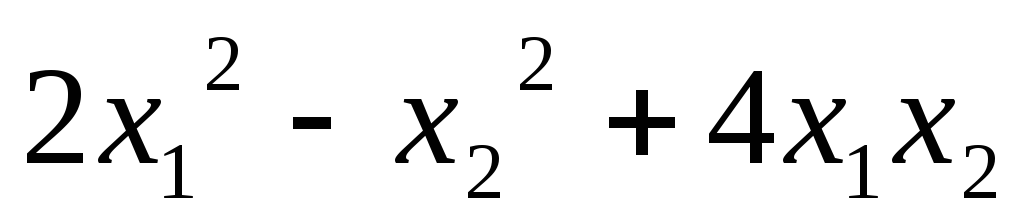 
;
5.2.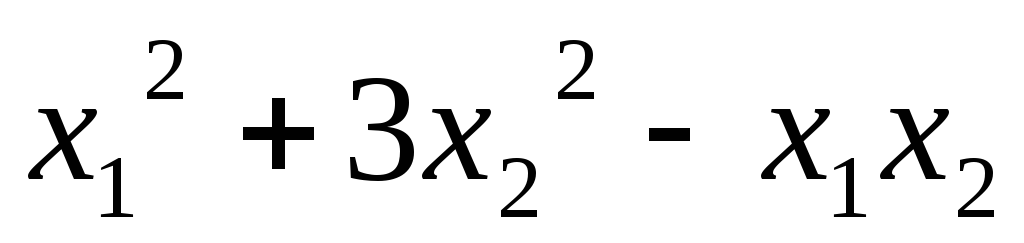 
;
5.3.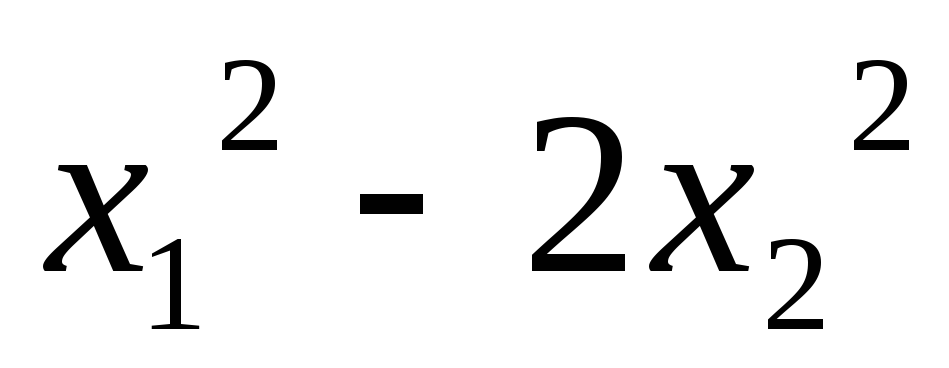 
;
5.4.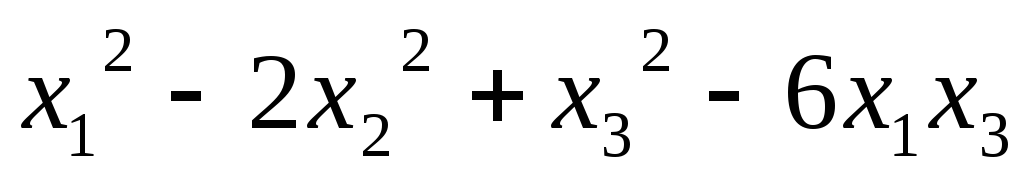 
;
5.5. 
;
5.6.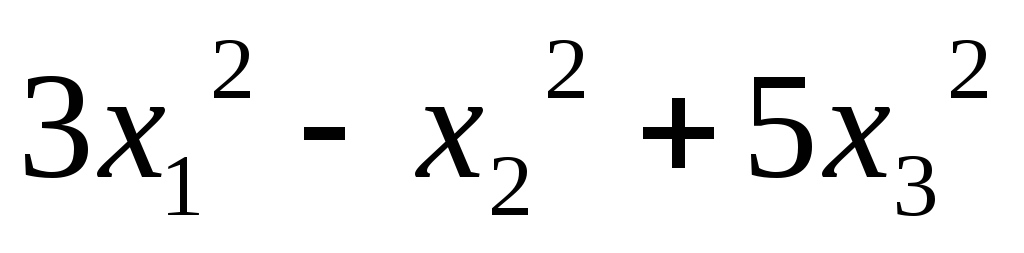 
;
5.7.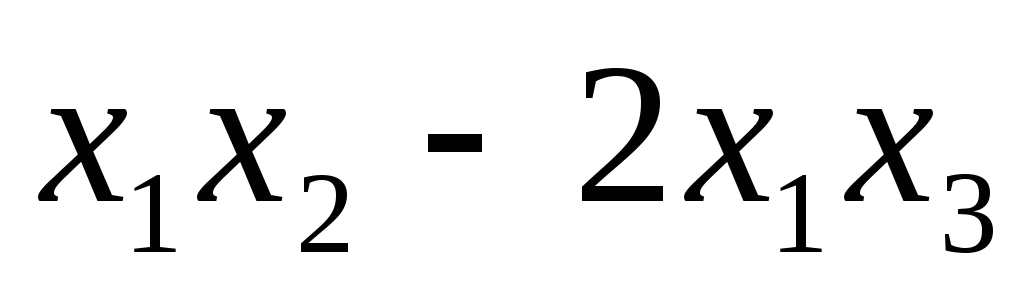 
;
5.8. 
;
5.9. 
;
5.10.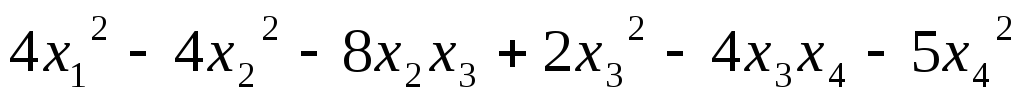 
;
5.11. .
Найти ранг квадратичной формы:
5.12.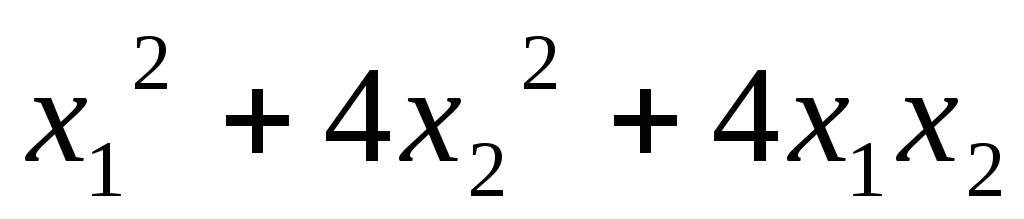 
;
5.13.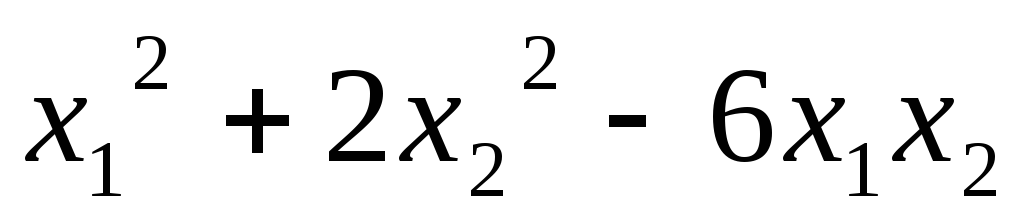 
;
5.14.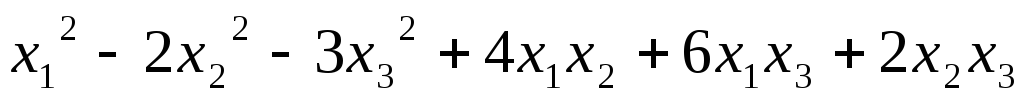 
;
114
5.15.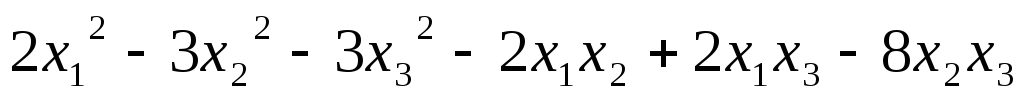 
;
5.16. 
;
5.17. 
;
5.18. 
;
5.19.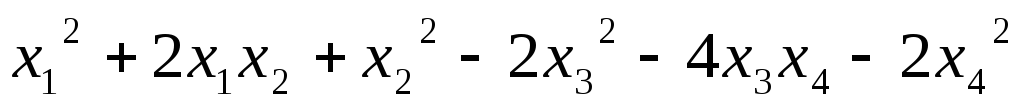 
;
5.20.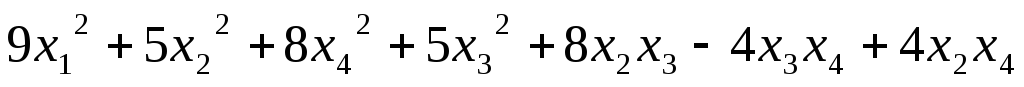 
.
Записать квадратичную форму в матричном виде:
5.21.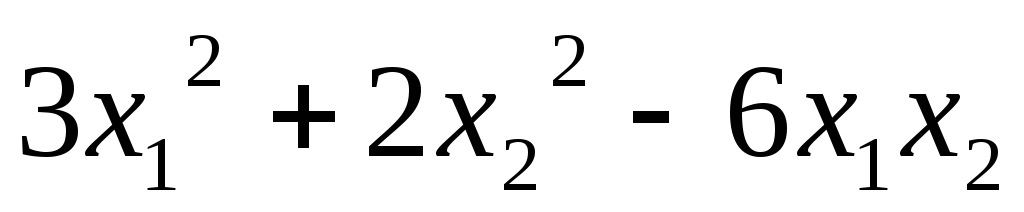 
;
5.22.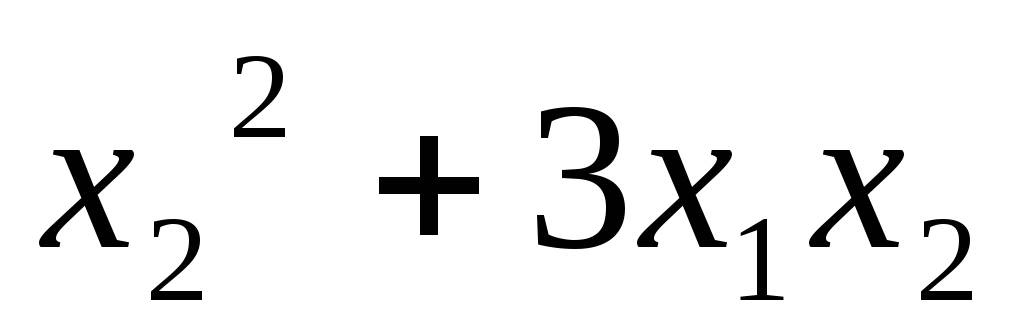 
;
5.23.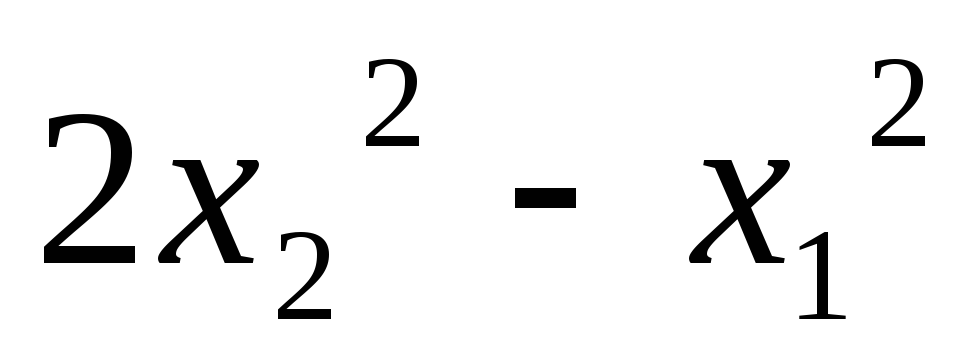 
;
5.24.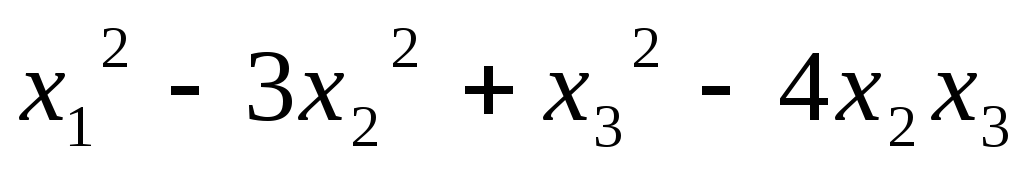 
;
5.25.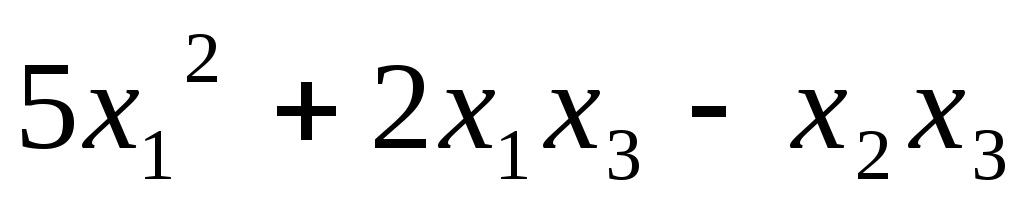 
;
5.26.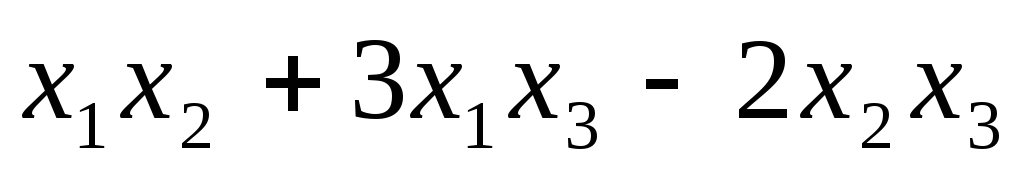 
;
5.27. 
;
5.28.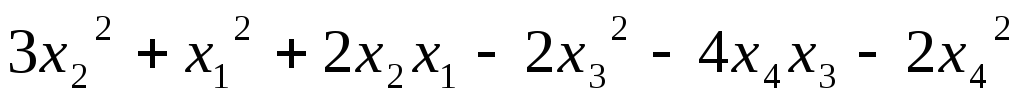 
;
5.29. ;
5.30.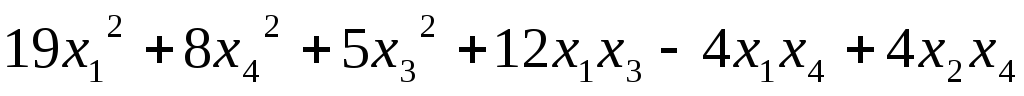 
.
Записать
квадратичную форму в виде 
по
заданной
матрице :
5.31. 
;
5.32. 
;
5.33. 
;
5.34.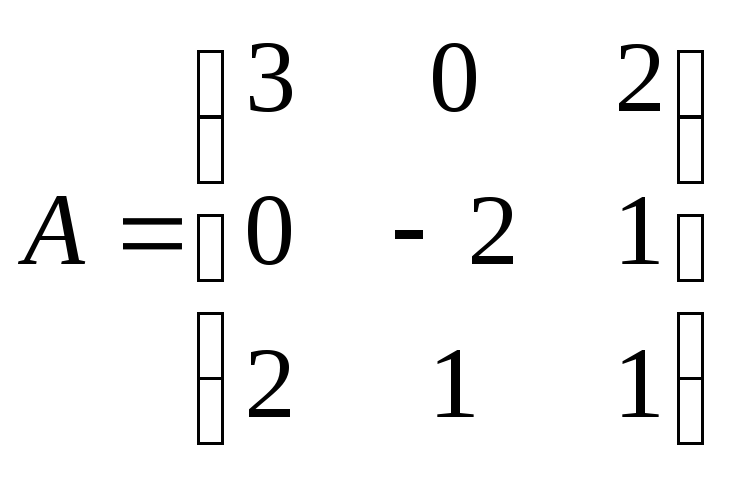 
;
115
5.35.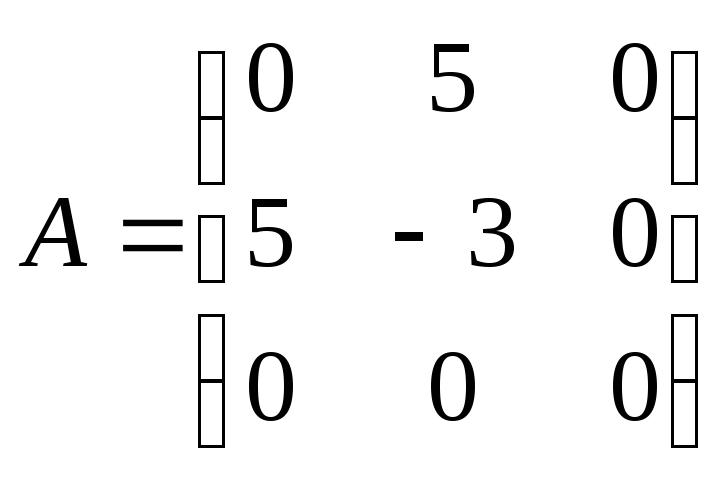 
;
5.36.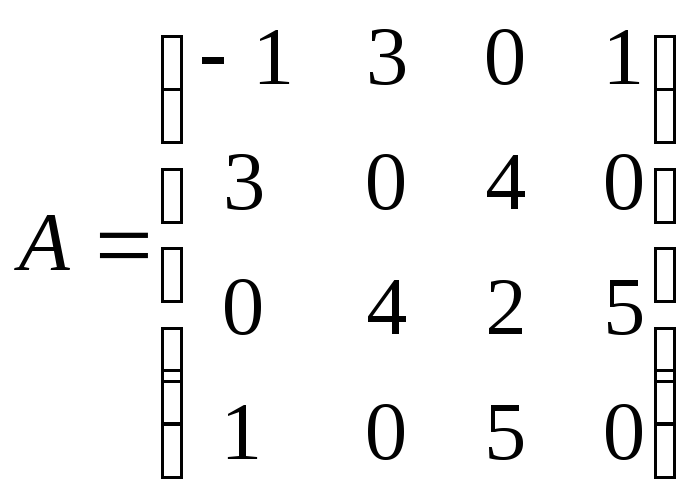 
;
5.37.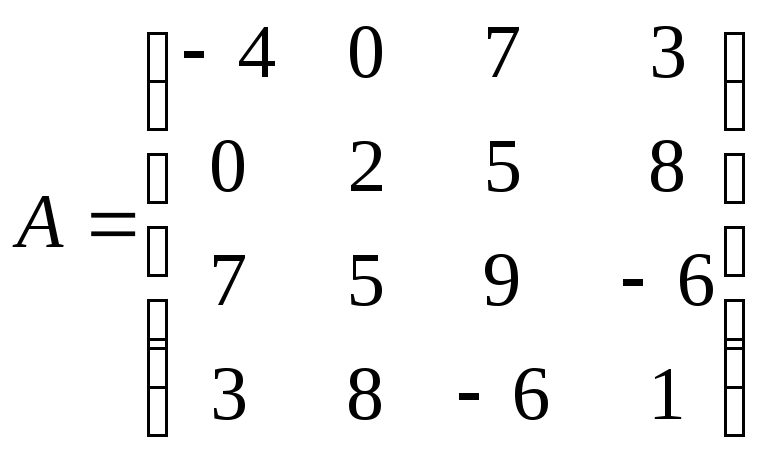 
;
5.38. 
;
5.39.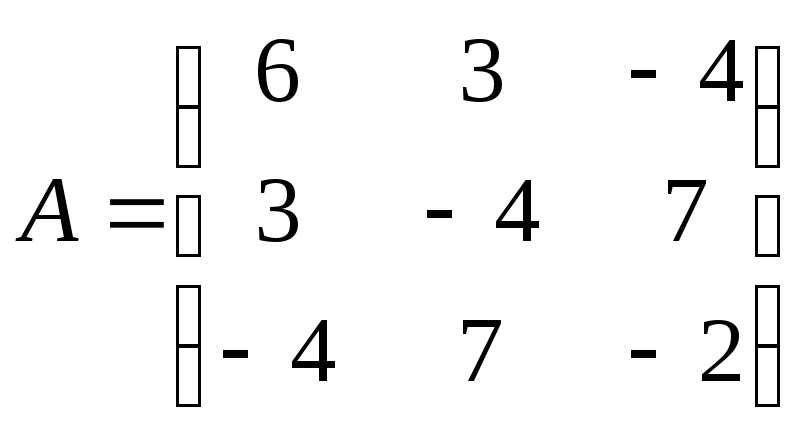 
;
5.40. 
.
Привести квадратичную форму к каноническому виду методом
Лагранжа и записать соответствующее преобразование:
5.41. 
;
5.42. 
;
5.43.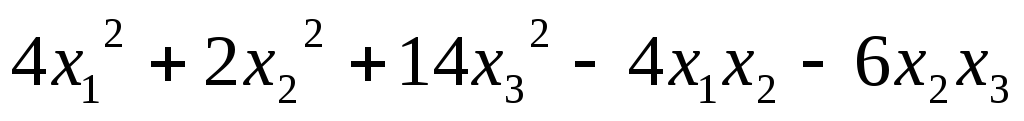 
;
5.44.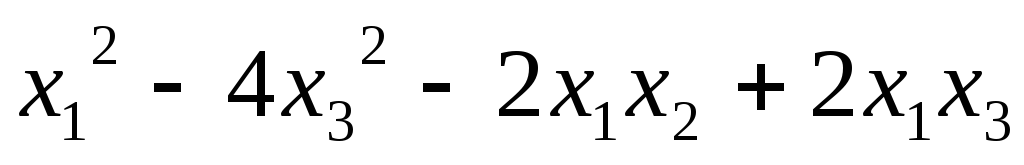 
;
5.45.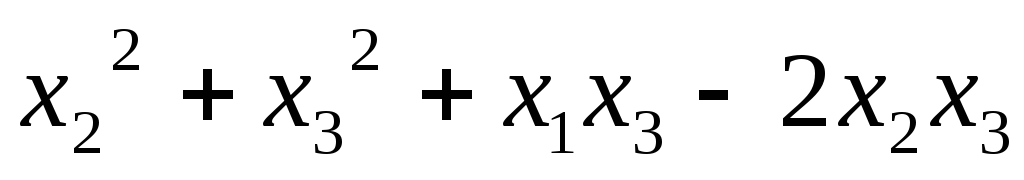 
;
5.46. 
;
5.47. 
5.48. 
5.49.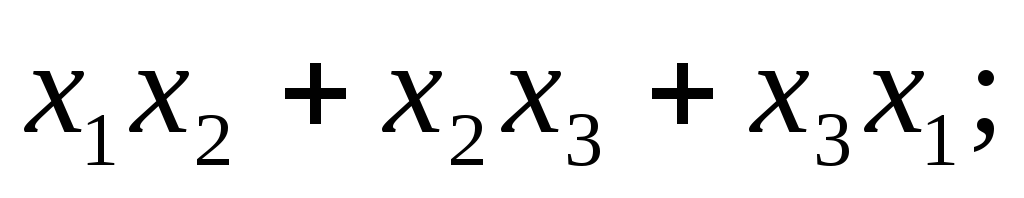 
5.50. 
5.51.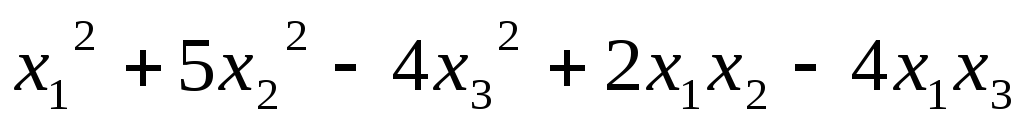 
;
116
5.52. 
.
Найти ортогональное преобразование, приводящее квадратичную
форму к каноническому виду и записать соответствующий кано-
нический вид квадратичной формы:
5.53.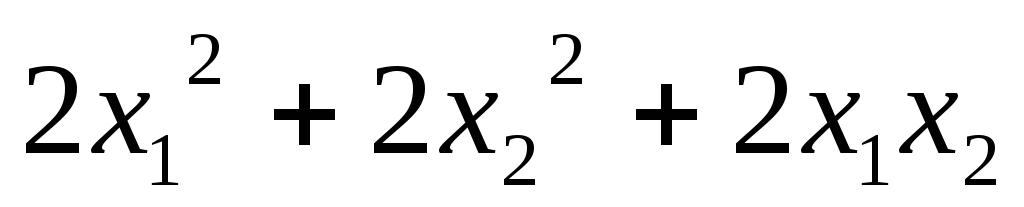 
;
5.54.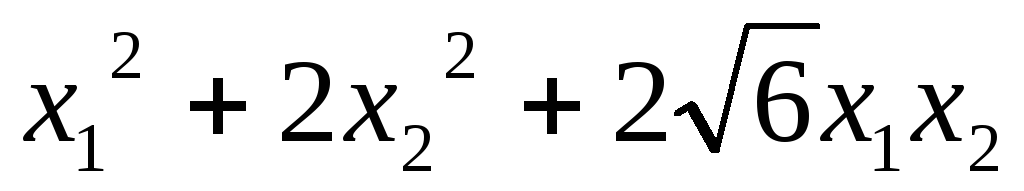 
;
5.55. 
;
5.56.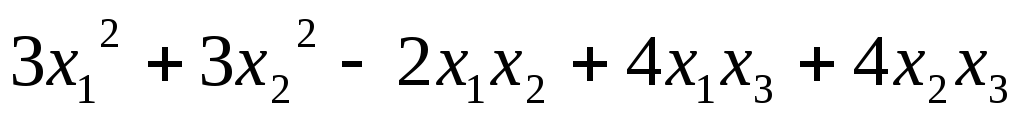 
;
5.57.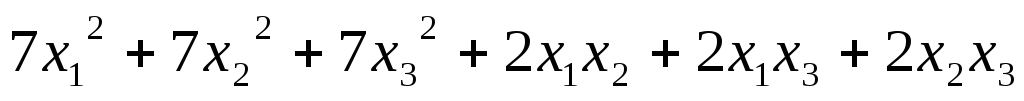 
;
5.58.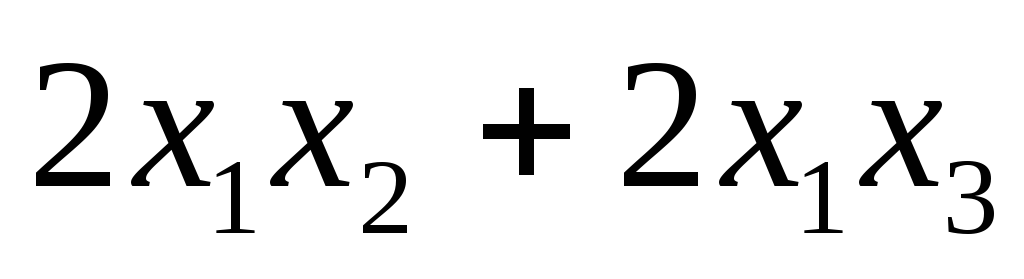 
;
5.59.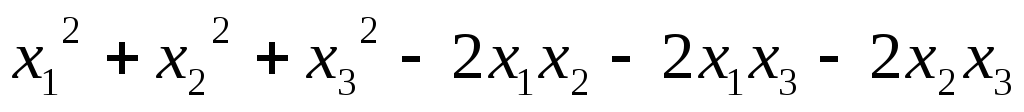 
;
5.60.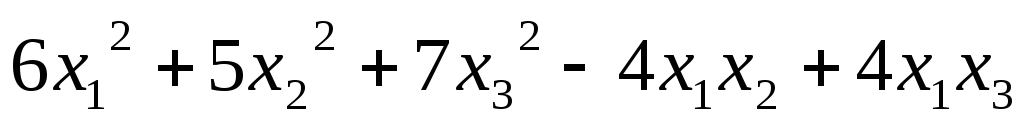 
;
5.61. 
;
5.62.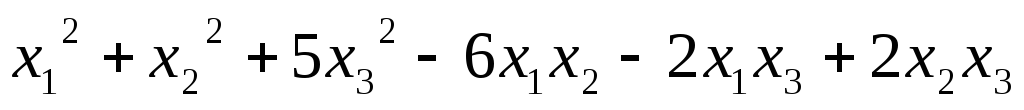 
.
Записать данное уравнение второго порядка в матричном виде и
определить, фигуру какого типа (эллиптического, гиперболическо-
го, параболического) оно определяет:
5.63. 
5.64.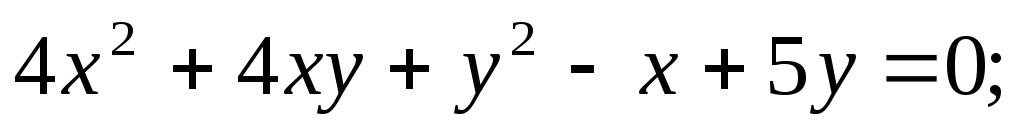 
5.65.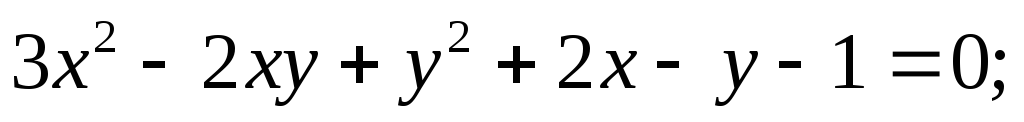 
5.66. 
5.67. 
5.68. 
5.69.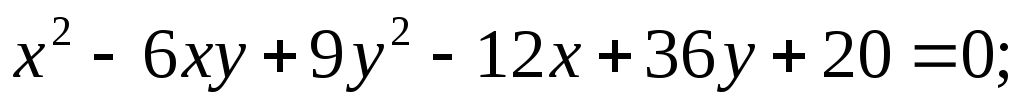 
5.70. 
5.71. 
5.72. 
117
5.73. 
5.74.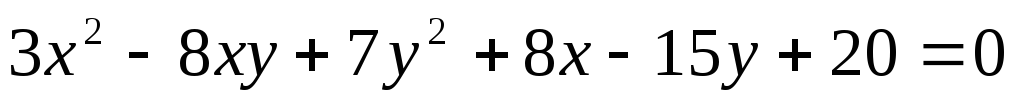 
.
Построить в прямоугольной системе координат Оху (O;i,j) фигуру,
определяемую данным уравне-нием, предварительно приведя его
к каноническому виду:
5.75.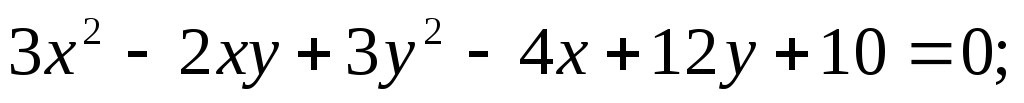 
5.76.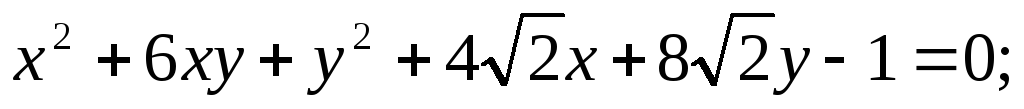 
5.77.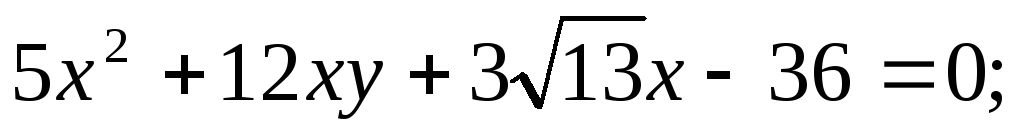 
5.78.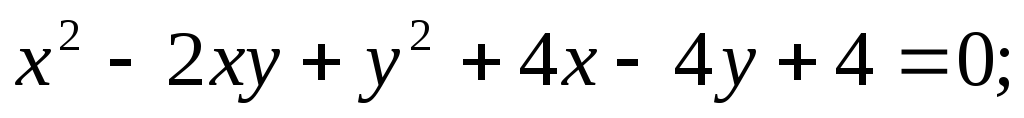 
5.79.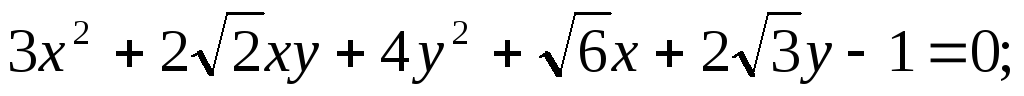 
5.80.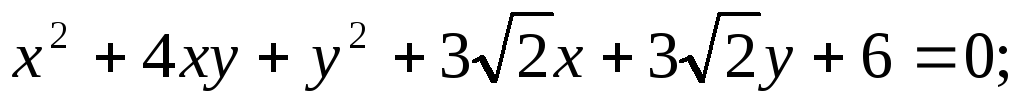 
5.81.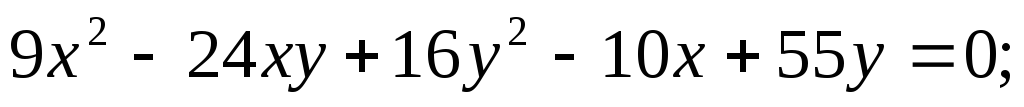 
5.82.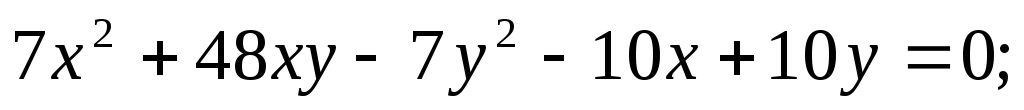 
5.83. 
5.84.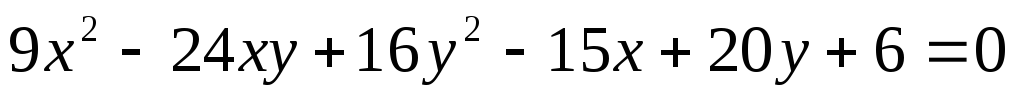 
.
Каждую из квадратичных форм исследовать на знакоопределённость
5.85. 
5.86. 
5.87. 
5.88. 
5.89.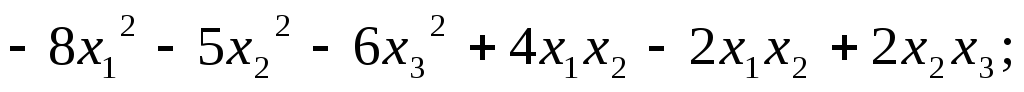 
5.90.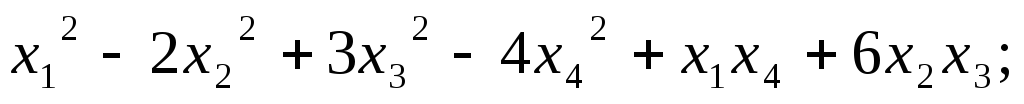 
5.91. 
5.92. 
5.93.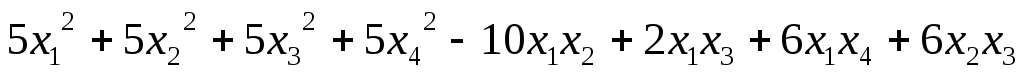 
;
5.94.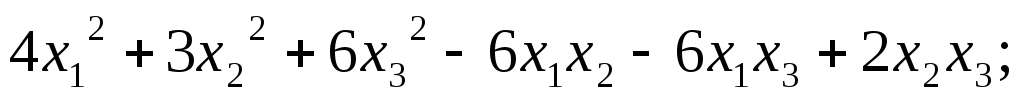 
118
5.95.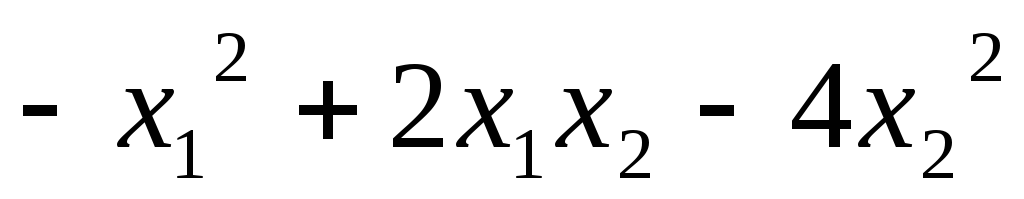 
;
5.96.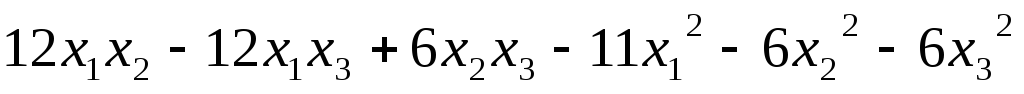 
.
119
Квадратичная форма — это… Что такое Квадратичная форма?
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Определение
Пусть есть векторное пространство над полем и — базис в .
Функция называется квадратичной формой, если её можно представить в виде
где , а — некоторые элементы поля .
Связанные определения
- Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.
Эквивалентные квадратичные формы
Две квадратичные формы и называются эквивалентными, если найдется целочисленная матрица:
с определителем равным 1, переводящая матрицу в матрицу :
Поскольку эквивалентное преобразование не меняет детерминант формы, необходимым условием эквивалентности двух форм является равенство их детерминантов. Однако обратное неверно: среди форм с одинаковым дискриминантом может найтись конечное число неэквивалентных.
Редуцированные квадратичные формы
Положим любое положительное целое число, не являющееся квадратом какого-либо другого целого числа. Каждый класс неопределенных квадратичных форм с дискриминантом содержит набор канонических представлений, называющихся редуцированными формами. Квадратичная форма называется редуцированной, если .
Так же нетрудно заметить, что квадратичная форма является редуцированной тогда и только тогда, когда и, что число редуцированных квадратичных форм определенного дискриминанта конечно.
Квадратные, смежные и неоднозначные квадратичные формы
Две формы и называются смежными, если выполняется условие , например:
Также на множестве эквивалентных форм можно определить операцию умножения(композицию) тогда, если коэффициенты и взаимно-просты,
Квадратной формой называется квадратичная форма вида , в которой третий коэффициент является полным квадратом. Из квадратичной формы можно извлечь квадратный корень. Для вычисления корня заменим форму на эквивалентную ей смежную форму , потом извлечем квадратный корень на основании предыдущего определения. В итоге операция извлечения корня сведется к следующему:
[1]
Форма вида называется неоднозначной. Если форма неоднозначна, то ее определитель делится на
Свойства
- Критерий Сильвестра
- Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
- Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
- Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.
- Для любой невырожденной квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:
- Разность между числом положительных () и отрицательных () членов в этой записи называется сигнатурой квадратичной формы. Сигнатура, также как и числа положительных и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра).
- Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа.
Примеры
Примечания
- ↑ Ш.Т. Ишмухаметов Методы факторизации натуральных чисел, Казанский университет, 2011 стр 78
Литература
- Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
- Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
- Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
- Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
- Беклемишев Д. В. Аналитическая геометрия и линейная алгебра.-М.: Высш. шк. 1998, 320с.
- Гельфанд И. М., Линейная алгебра. Курс лекций.
- Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.
Первая квадратичная форма — Википедия
Материал из Википедии — свободной энциклопедии
Первая квадратичная форма (или первая фундаментальная форма или метрический тензор) поверхности ― квадратичная форма на касательном расслоении поверхности, которая определяет внутреннюю геометрию поверхности в окрестности данной точки. Первая квадратичная форма часто обозначается I{\displaystyle \mathrm {I} }.
Знание первой квадратичной формы достаточно для вычисления гауссовой кривизны поверхности, а также для вычисления длин дуг, углов между кривыми и площади областей на поверхности.
Пусть в евклидовом пространстве со скалярным произведением ⟨⋅,⋅⟩{\displaystyle \langle \cdot ,\cdot \rangle } поверхность задана уравнением r=r(u,v),{\displaystyle r=r(u,v),} где u{\displaystyle u} и v{\displaystyle v} ― внутренние координаты на поверхности; dr=rudu+rvdv{\displaystyle dr=r_{u}du+r_{v}dv} ― дифференциал радиус-вектора r{\displaystyle r} вдоль выбранного направления смещения из точки M{\displaystyle M} в бесконечно близкую точку M′{\displaystyle M’}. (Здесь ru{\displaystyle r_{u}} и rv{\displaystyle r_{v}} — частные производные радиус-вектора r{\displaystyle r} по u{\displaystyle u} и по v{\displaystyle v} соответственно.) Тогда квадрат главной части приращения длины |MM′|{\displaystyle |MM’|} выражается квадратом дифференциала dr{\displaystyle dr}:
- I=(dr)2=⟨ru,ru⟩du2+2⟨ru,rv⟩dudv+⟨rv,rv⟩dv2{\displaystyle \mathrm {I} =(dr)^{2}=\langle r_{u},r_{u}\rangle du^{2}+2\langle r_{u},r_{v}\rangle dudv+\langle r_{v},r_{v}\rangle dv^{2}}
и называется первой квадратичной формой поверхности.
Коэффициенты первой квадратичной формы обычно обозначают через
- E=|ru|2, F=⟨ru,rv⟩, G=|rv|2{\displaystyle E=|r_{u}|^{2},\ F=\langle r_{u},r_{v}\rangle ,\ G=|r_{v}|^{2}}
или, в тензорных символах,
- I=dr2=g1,1du2+2g1,2dudv+g2,2dv2.{\displaystyle \mathrm {I} =dr^{2}=g_{1,1}du^{2}+2g_{1,2}dudv+g_{2,2}dv^{2}.}
Тензор gi,j{\displaystyle g_{i,j}} называется основным, или метрическим, тензором поверхности.
- Первая квадратичная форма является положительно определенной формой в обыкновенных точках поверхности; в частности
- EG−F2>0.{\displaystyle EG-F^{2}>0.}
- Мищенко А.С. Фоменко А.Т. Курс дифференциальной геометрии и топологии. — Физматлит, 2004. — ISBN 5-9221-0442-X.
- Топоногов В.А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 9785891552135.
ФОРМА КВАДРАТ НА НАТУРАЛЬНЫХ НОГТЯХ
В этой статье я вам расскажу, как придать натуральным ногтям квадратную форму, форму мягкий квадрат и квадрат с закругленными краями. Объясню отличия этих форм и нюансы опила.
Для того, чтобы подпилить натуральный ноготь, с ногтевой пластины должно быть снято искусственное покрытие. Для опила мне понадобится пилочка 100/180 грит, у меня она тоненькая на деревянной основе.
Шаг 1. Возьму в руки пилку удобным для меня захватом. Большой палец у меня находится с одной стороны, а четыре остальных с другой.
Шаг 2. Сначала я подпилю ноготь с двух боков. Пилку необходимо держать перпендикулярно относительно натурального ногтя и опиливать только свободный край, иначе можно истончить и повредить боковые части натурального ногтя. Хочу обратить внимание, что подпиливать боковые части нужно таким образом, чтобы точка выхода ногтевой пластины была ровной и при отрастании ногтя не было ступеней между опиленным краем и отросшим.
Правильная постановка пилки для опила натурального ногтя
Неправильная постановка пилки. Применяется для опила искусственного ногтя
Шаг 3. Теперь я подпилю торцевую часть ногтевой пластины.
- Для придания ногтю формы квадрат, пилку я держу строго перпендикулярно ногтевой пластине. Чтобы уголки не кололись и не мешали, я их слегка подпилю мягкой стороной пилки (буквально пару движений).
- Для придания формы мягкий квадрат необходимо у квадрата спилить углы. Для этого я подставляю пилку под углом к ногтевой пластине и подпилю уголки.
- Для придания формы ногтя квадрат с закругленными углами необходимо у квадрата закруглить углы.
Шаг 4. После подпиливания ногтевой пластины, обратной стороной пушера я прочищаю под ногтем и убираю остатки опила, иначе в дальнейшем могут появиться отслойки гель-лака.
Шаг 5. Теперь мягкой стороной пилки я зашлифовываю торец и окончательно убираю остатки опила.
Работа по подпиливанию ногтевых пластин окончена.
С вами была Ирина Набок.
До новых встреч.
Читайте также:
Полезные ссылки:
◉ Акригель LadyMistry 30 ml ► http://ali.pub/29s7l4
◉ Акригель LadyMistry 60 ml ► http://ali.pub/29s7t3
◉ Акригель MSHARE ► http://ali.pub/27tlxe ► http://got.by/27tlxe
◉ Кисть для Акригеля ► http://ali.pub/27tm47 ► http://got.by/27tm47
◉ Гель Лаки Fiore > https://vk.cc/7jSgYo
◉ Мебель маникюр (Подставка под руку, столы) https://vk.com/mebel_manikur и инстаграм @mebel_manikur Скидка 10% по купону GRANDNAIL
◉ Магазин Евромедсервис: Аппараты для маникюра и педикюра http://bit.ly/21onYVm
Магазин предоставил скидку моим подписчикам 15% ПРОМОКОД GRAND15
◉ Лампы Sun в магазине, где покупаю я > http://ali.pub/mc8hn
Оцените статью и спрашивайте, если остались вопросы
comments powered by HyperComments
Новые Курсы Ирины Набок
Наращивание и Коррекция на Верхние Формы Акригелем с правильной конструкцией
от 4 900 руб
Работа колпачками в маникюре Мини курс
3500руб
990 руб
Онлайн Курсы GRAND NAIL
Современный Гель лак
15700руб
7 800 руб
Курс Наращивания и Коррекции Ногтей Акригелем (Полигелем)
29500руб
17 500 руб
Базовые знания о материалах для покрытия и наращивания ногтей 2019
Видео-семинар Ирины Набок
1 200 руб
Онлайн Практикумы — GRAND NAIL
Новая технология укрепления натуральных ногтей
от 4 000 РУБ
Наращивание и коррекция ногтей Акригелем Квадрат
от 4000 РУБ
Наращивание и коррекция ногтей Акригелем Овал
от 4000 РУБ
Без опила. Техника работы с твердыми материалами
от 4000 РУБ
Выкладной Френч Акригель
от 4000 РУБ
Исправление Клювовидных или Внизрастущих ногтей
1790 РУБ
Онлайн Курсы Дизайна Ногтей — GRAND NAIL
MAGIC FLOWERS
Курс дизайна ногтей
от 3 000 руб
АКВАРЕЛЬ
Курс дизайна ногтей
от 3 000 руб
DREAM WHITE
Курс дизайна ногтей
от 3 000 руб
ЮВЕЛИРНЫЙ
Курс дизайна ногтей
от 3 000 руб
КРУЖЕВНЫЕ ФАНТАЗИИ
Курс дизайна ногтей
от 3 000 руб
АЭРОПУФФИНГ
Курс дизайна ногтей
от 3 000 руб
КУРС ИДЕАЛЬНЫЕ ВЕНЗЕЛЯ
7000руб
4 900 руб
Закрытая группа
Дизайна ногтей Юлии Матюхиной
990 руб/месяц
Курсы по санитарной безопасности
БЕЗОПАСНЫЙ МАНИКЮР 2.0
КУРС О ЗАБОЛЕВАНИЯХ НОГТЕЙ, КОЖИ КИСТЕЙ И СТОП
от 3000 РУБ
Предложения со словосочетанием ФОРМУ КВАДРАТА
Нарезать хлеб в форме квадратов со сторонами 5 см, посыпать их сыром, полить сливками, накрыть кусочками сала и поместить кусочки в порционные горшочки. Кабинет имел форму квадрата. Для этой цели применяются не цельные зеркала (это было бы слишком дорого и непрактично), а зеркальные плитки, представляющие собой отдельные зеркала в форме квадратов, размером примерно 25 х 25 см. При этом у него на данном занятии развиваются элементарные навыки переноса: шар — отверстие круглой формы — окошко, куб — отверстие квадратной формы — квадрат. Сам дастархан походил на сколоченный из досок неправильной формы квадрат, примерно, три на три метра, лежащий на нескольких широких чурбанах.
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: проступать — это что-то нейтральное, положительное или отрицательное?
Положительное
Отрицательное
Садовники всё ни как не могли оставить в покое кусты с белыми листьями и серыми цветами, стараясь придать им, казалось, простую форму квадрата. Форма квадрата на психологическом уровне вызывает ощущение прочности и стабильности, поэтому символ квадрат так распространён в качестве символа строительства. Перед подачей омлет нарезаем на порции в форме квадрата, прямоугольника или ромба. Так, всё знают, как застелить пол плитками в форме квадратов или равносторонних шестиугольников, но такое возможно и в случае с равносторонними пятиугольниками. Именно потому, что круг будет «стремиться» к форме квадрата, а квадрат будет противостоять стремлению сферы придать этому квадрату форму круга. Оно имело форму квадрата и ступенями поднималось прямо из воды. Раскатайте тесто в форме квадрата, в середину положите масло. Чашечки поддерживают специальные глиняные подставочки в форме квадрата с закруглёнными краями. Каравелла представляла собой новый тип океанского судна, в котором эффективно сочетались паруса в форме квадрата и треугольника, что позволяло максимально использовать силу ветра, в том числе и встречного. Нарезать на небольшие ломтики в форме квадратов, загарнировать и поджарить на масле до золотистого цвета. Дзен-буддисты полагали, что формы бытия взаимопроникаемы друг в друга, поэтому можно вернуться к исходной форме квадрата или создать из неё другую фигурку. Батон нарезать на 8 тонких ломтиков, придав им форму квадрата. Намазать хлеб маслом, затем селёдочным паштетом, посыпать мелкорубленой зеленью петрушки. Если вы выбрали в качестве своей основной формы квадрат, то вы — неутомимый труженик! Ячейки для стёкол в этих окнах были заметно крупнее и имели форму квадрата. Четыре располагаются в форме квадрата, а пятая посредине. У неё было четыре буквы и она разместила их в форме квадрата. Центр шахматной доски имеет форму квадрата. Он имел форму квадрата с четырьмя бастионами на углах квадрата. Они имеют форму квадрата, и их высота составляет около 30 см, а глубина — около 15 см. В плане эти храмы имели форму квадрата с четырьмя контрфорсами по углам и были окружены мощёным двором, частично затенённым крышей, опирающейся на столбы. Так, например, часть кирпича, нижняя и верхняя постели которого имеют форму квадрата, называется три четверти; расколотый пополам по всей длине кирпич образует длинные половины. Призматические раздвижные плашки состоят из двух полуплашек и имеют форму квадрата. Их также применяют при нарезании резьбы. В одном из малых дворов размещена четырёхэтажная, в форме квадрата башня. Песок на том месте, где они только что стояли, раздвинулся, образовав небольшой кратер в форме квадрата. Например, амулет, охраняющий голову владельца, обычно изготавливался из гематита в форме квадрата. Для этого ячея должна быть не в форме ромба, горизонтальная ось которого равняется длине стороны (как при стандартной посадке ставной сети), а в форме квадрата — в ячею такой формы рыба меньше путается. На одном листе вкруг по радиусам были распределены все отделы, подотделы и секции, а на другом листе то же самое было сделано в форме квадратов. Тесто вокруг фарша плотно прижмите и с помощью ножа вырежите пельмени в форме квадратов таким образом, чтобы начинка оказалась посередине. Оборудование: большой белый лист в форме квадрата со стороной 30 см. Во дворе необходимо расчистить ровную площадку в форме квадрата площадью примерно в 4 кв. Двор имел форму квадрата с высокой башней — или колокольней — в своей северной части и с входной дверью с южной стороны. Нет, поначалу я прошлась по комнате, имевшей форму квадрата, и даже сумела рассмотреть ещё две двери, ведущие неизвестно куда. Но на них не было ручек! Им, выдали нагрудные знаки отличия, имеющие форму квадрата, на котором изображены два треугольника составляющих ромб, а также застёжки на браслеты десантников, такой же формы. Деревянное сооружение в форме квадрата с крошечными башенками по углам. В центре пола различался правильной формы квадрат метр на метр, заложенный густой решёткой. Холодное тесто очень быстро (пока оно не успело согреться) раскатай в форме квадрата, в середину положи масло. Достаточно сказать, что один из бассейнов имел форму квадрата, сторона которого равнялась полутора километрам, а всего таких бассейнов было три. В фэн-шуй используются вогнутые и выгнутые зеркала, с помощью которых вы можете видимо увеличить или уменьшить помещение, придав ему форму квадрата. Селихов к двум корпусам богадельни пристроил ещё два, после возведения которых двухэтажное здание богадельни стало иметь форму квадрата. Temenos обычно имел форму квадрата или прямоугольника, но даже если форма была и неправильной, стороны всё равно оставались прямыми. Нижний этаж имел форму квадрата со сторонами около 200 м и представлял собой своеобразный дворец. Лицо анфас имеет форму квадрата и сужается по краям наподобие призмы.